Subcategory
A particular case of the concept of a substructure of a mathematical structure. A category 
is called a subcategory of a category 
if 
,
 |
for any 
and if the composite of two morphisms in 
coincides with their composite in 
. For each subclass 
of 
there are smallest and largest subcategories 
and 
of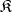 
whose classes of objects coincide with 
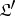; the subcategory 
contains only identity morphisms of objects in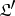 
and is called the discrete subcategory generated by 
; the subcategory 
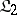contains all morphisms in 
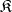with domain and codomain in 
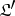and is called the full subcategory generated by 
. Any subcategory 
of 
for which 
for any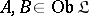 
is called a full subcategory of 
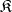. The following are full subcategories: the subcategory of non-empty sets in the category of all sets, the subcategory of Abelian groups in the category of all groups, etc. For a small category 
, the full subcategory of the category of all contravariant functors from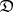 
into the category of sets generated by the hom-functors (morphism functors, 
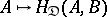) is isomorphic to 
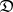(cf. also Functor). This result enables one to construct the completion of an arbitrary small category with respect to limits or co-limits.
An arbitrary subcategory of a category 
need not inherit any of the properties of this category. However, there are important classes of subcategories that inherit many properties of the ambient category, such as reflective subcategories (cf. Reflective subcategory) and co-reflective subcategories.
Subcategory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Subcategory&oldid=17402