Sturm theorem
If
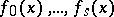 | (*) |
is a Sturm series on the interval  ,
,  , and
, and  is the number of variations of sign in the series (*) at a point
is the number of variations of sign in the series (*) at a point  (vanishing terms are not taken into consideration), then the number of distinct roots of the function
(vanishing terms are not taken into consideration), then the number of distinct roots of the function  on the interval
on the interval  is equal to the difference
is equal to the difference  .
.
A Sturm series (or Sturm sequence) is a sequence of real-valued continuous functions (*) on  having a finite number of roots on this interval, and such that
having a finite number of roots on this interval, and such that
1) 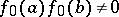 ;
;
2) 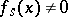 on
on 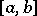 ;
;
3) from 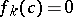 for some
for some 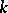
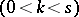 and given
and given  in
in 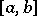 it follows that
it follows that 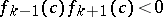 ;
;
4) from 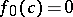 for a given
for a given 
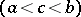 it follows that for sufficiently small
it follows that for sufficiently small  ,
,
 |
 |
This theorem was proved by J.Ch. Sturm [1], who also proposed the following method of constructing a Sturm series for a polynomial 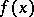 with real coefficients and without multiple roots:
with real coefficients and without multiple roots: 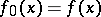 ,
, 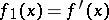 , and, if the polynomials
, and, if the polynomials 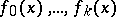 are already constructed, then as
are already constructed, then as 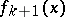 one should take minus the remainder occurring in the process of dividing
one should take minus the remainder occurring in the process of dividing 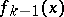 by
by 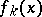 . Here,
. Here,  will be a non-zero constant.
will be a non-zero constant.
References
| [1] | J.Ch. Sturm, Bull. de Férussac , 11 (1829) |
| [2] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) |
Comments
The coefficients of the polynomials in the Sturm series must belong to a real-closed field. The algorithm to determine a Sturm series for a polynomial  can be described as follows:
can be described as follows:
 |
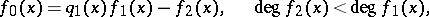 |
 |
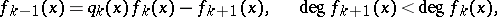 |
 |
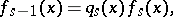 |
so 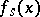 is a non-zero constant.
is a non-zero constant.
References
| [a1] | N. Jacobson, "Basic algebra" , I , Freeman (1974) |
| [a2] | L.E.J. Dickson, "New first course in the theory of equations" , Wiley (1939) |
| [a3] | B.L. van der Waerden, "Algebra" , 1 , Springer (1967) (Translated from German) |
Sturm theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sturm_theorem&oldid=17606