Sturm-Liouville equation
An ordinary differential equation of the second order
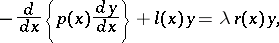 |
where  varies in a given finite or infinite interval
varies in a given finite or infinite interval 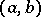 ,
, 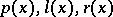 are given coefficients,
are given coefficients, 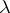 is a complex parameter, and
is a complex parameter, and 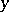 is the sought solution. If
is the sought solution. If 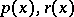 are positive,
are positive, 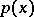 has a first derivative and
has a first derivative and 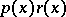 has a second derivative, then by the Liouville substitution (see [1]) this equation may be reduced to the standard form
has a second derivative, then by the Liouville substitution (see [1]) this equation may be reduced to the standard form
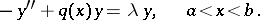 | (1) |
It is assumed that the complex function 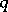 is measurable on
is measurable on  and summable on each of the subintervals in it. At the same time one also considers the non-homogeneous equation
and summable on each of the subintervals in it. At the same time one also considers the non-homogeneous equation
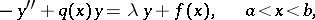 | (2) |
where 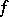 is a given function.
is a given function.
If 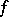 is measurable on
is measurable on 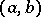 and summable on each of the subintervals in it, then for all complex numbers
and summable on each of the subintervals in it, then for all complex numbers 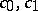 and any interior point
and any interior point 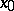 , equation (2) has on
, equation (2) has on 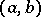 one and only one solution
one and only one solution 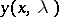 satisfying the conditions
satisfying the conditions 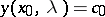 ,
, 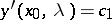 . For any
. For any 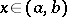 the function
the function 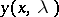 is an entire analytic function of
is an entire analytic function of 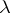 . As
. As 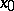 one can take one of the end-points of
one can take one of the end-points of 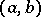 (if this end-point is regular, cf. Sturm–Liouville operator).
(if this end-point is regular, cf. Sturm–Liouville operator).
Let 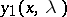 and
and  be two arbitrary solutions of (1). Their Wronskian
be two arbitrary solutions of (1). Their Wronskian
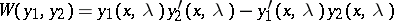 |
is independent of  and vanishes if and only if these solutions are linearly dependent. The general solution of (2) is of the form
and vanishes if and only if these solutions are linearly dependent. The general solution of (2) is of the form
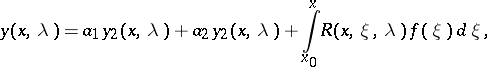 |
where
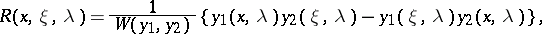 |
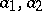 are arbitrary constants and
are arbitrary constants and 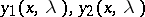 are linearly independent solutions of (1).
are linearly independent solutions of (1).
The following fundamental theorem of Sturm (see [1]) is true: Let two equations
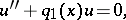 | (3) |
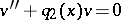 | (4) |
be given. If 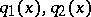 are real and
are real and 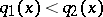 on the entire interval
on the entire interval 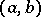 , then between any two zeros of any non-trivial solution of the first equation there is at least one zero of each solution of the second equation.
, then between any two zeros of any non-trivial solution of the first equation there is at least one zero of each solution of the second equation.
The following theorem is known as the comparison theorem (see [1]): Let the left-hand end-point of  be finite, let
be finite, let 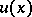 be a solution of (3) satisfying the conditions
be a solution of (3) satisfying the conditions 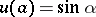 ,
, 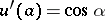 , and let
, and let 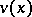 be a solution of (4) with the same conditions; let, moreover,
be a solution of (4) with the same conditions; let, moreover,  on the whole interval
on the whole interval 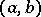 . Then, if
. Then, if 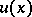 has
has 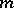 zeros on
zeros on 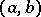 ,
, 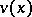 will have at least
will have at least 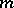 zeros and the
zeros and the 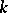 -th zero of
-th zero of 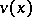 will be less than the
will be less than the 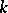 -th zero of
-th zero of 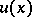 .
.
One of the important properties of (1) is the existence of so-called operator transforms with a simple structure. Operator transforms arose from general algebraic considerations related to the theory of generalized shift operators (change of the basis).
There are the following types of operator transforms for equation (1). Let 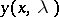 be the solution of
be the solution of
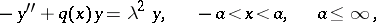 | (5) |
satisfying the conditions
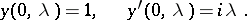 | (6) |
It turns out that this solution has the following representation:
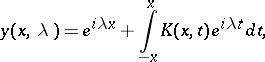 |
where 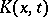 is a continuous function independent of
is a continuous function independent of 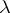 ; moreover,
; moreover,
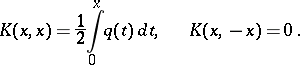 |
The integral operator 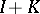 defined by
defined by
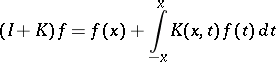 |
is called an operator transform (a transmutation operator), and preserves the conditions at the point 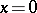 . It transforms the function
. It transforms the function 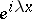 (a solution of the simplest equation
(a solution of the simplest equation 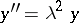 with the conditions (6)) into the solution of (5) under the same conditions at the point
with the conditions (6)) into the solution of (5) under the same conditions at the point 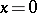 . Let
. Let 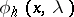 and
and 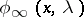 be the solutions of (5) satisfying
be the solutions of (5) satisfying
 |
 |
These solutions have the representations
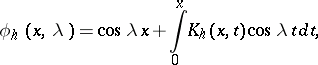 |
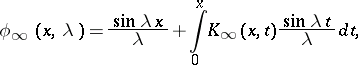 |
where 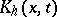 and
and 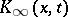 are continuous functions.
are continuous functions.
A new type of operator transforms has been introduced (see [8]) that preserves the asymptotic behaviour of solutions at infinity; namely, it turned out that for all 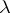 in the upper half-plane,
in the upper half-plane, 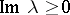 , the equation (5), considered on the half-line
, the equation (5), considered on the half-line 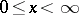 under the conditions
under the conditions 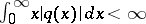 , has a solution
, has a solution 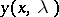 that can be represented in the form
that can be represented in the form
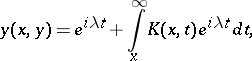 |
where 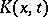 is a continuous function satisfying the inequality
is a continuous function satisfying the inequality
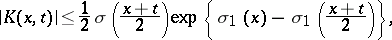 |
in which
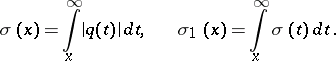 |
Moreover,
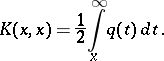 |
References
| [1] | B.M. Levitan, I.S. Sargsyan, "Introduction to spectral theory: selfadjoint ordinary differential operators" , Amer. Math. Soc. (1975) (Translated from Russian) |
| [2] | M.A. Naimark, "Lineare Differentialoperatoren" , Akademie Verlag (1960) (Translated from Russian) |
| [3] | B.M. Levitan, "Generalized translation operators and some of their applications" , Israel Program Sci. Transl. (1964) (Translated from Russian) |
| [4] | V.A. Marchenko, "Sturm–Liouville operators and applications" , Birkhäuser (1986) (Translated from Russian) |
| [5] | J. Delsarte, "Sur certaines transformations fonctionnelles rélatives aux équations linéaires aux dérivées partielles du second ordre" C.R. Acad. Sci. Paris , 206 (1938) pp. 1780–1782 |
| [6] | A.Ya. Povzner, "On Sturm–Liouville type differential equations on the half-line" Mat. Sb. , 23 : 1 (1948) pp. 3–52 (In Russian) |
| [7] | B.M. Levitan, "The application of generalized shift operators to linear second-order differential equations" Uspekhi Mat. Nauk , 4 : 1 (1949) pp. 3–112 (In Russian) |
| [8] | B.Ya. Levin, "Transformations of Fourier and Laplace types by means of solutions of second order differential equations" Dokl. Akad. Nauk SSSR , 106 : 2 (1956) pp. 187–190 (In Russian) |
| [9] | B.M. Levitan, "Inverse Sturm–Liouville problems" , VNU (1987) (Translated from Russian) |
Comments
References
| [a1] | R. Carroll, "Transformation theory and application" , North-Holland (1985) |
| [a2] | B.M. Levitan, I.S. Sargsyan, "Sturm–Liouville and Dirac operators" , Kluwer (1991) (Translated from Russian) |
Sturm-Liouville equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sturm-Liouville_equation&oldid=16467