Namespaces
Variants
Actions

Difference between revisions of "Student distribution"

From Encyclopedia of Mathematics
Jump to: navigation, search
m (tex encoded by computer)
m (Undo revision 48882 by Ulf Rehmann (talk))
Tag: Undo
Line 1: Line 1:
−
<!--
+
''with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907102.png" /> degrees of freedom, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907104.png" />-distribution''
−
s0907102.png
 
−
$#A+1 = 49 n = 0
 
−
$#C+1 = 49 : ~/encyclopedia/old_files/data/S090/S.0900710 Student distribution
 
−
Automatically converted into TeX, above some diagnostics.
 
−
Please remove this comment and the {{TEX|auto}} line below,
 
−
if TeX found to be correct.
 
−
-->
 
−
 
 
−
{{TEX|auto}}
 
−
{{TEX|done}}
 
−
 
 
−
''with  $  f $
 
−
degrees of freedom, $  t $-
 
−
distribution''
 
  
 
The probability distribution of the random variable
 
The probability distribution of the random variable
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907105.png" /></td> </tr></table>
−
t _ {f}  =
 
−
\frac{U}{\sqrt {\chi _ {f}  ^ {2} / f } }
 
−
,
 
−
$$
 
−
 
 
−
where  $  U $
 
−
is a random variable subject to the standard normal law  $  N( 0, 1) $
 
−
and  $  \chi _ {f}  ^ {2} $
 
−
is a random variable not depending on  $  U $
 
−
and subject to the [[Chi-squared distribution| "chi-squared" distribution]] with  $  f $
 
−
degrees of freedom. The distribution function of the random variable  $  t _ {f} $
 
−
is expressed by the formula
 
  
−
$$
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907106.png" /> is a random variable subject to the standard normal law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907107.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907108.png" /> is a random variable not depending on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s0907109.png" /> and subject to the [[Chi-squared distribution| "chi-squared" distribution]] with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071010.png" /> degrees of freedom. The distribution function of the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071011.png" /> is expressed by the formula
−
{\mathsf P} \{ t _ {f} \leq  x \} = S _ {f} ( x) =
 
−
$$
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071012.png" /></td> </tr></table>
−
= \
 
  
−
\frac{1}{\sqrt {\pi _ {f} } }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071013.png" /></td> </tr></table>
−
 
−
\frac{\Gamma ( ( f+ 1 ) / 2 ) }{\Gamma
 
−
( f / 2 ) }
 
−
\int\limits _ {- \infty } ^ { x }  \left ( 1 +
 
−
\frac{u
 
−
^ {2} }{f}
 
−
\right ) ^ {- ( f+ 1 ) / 2 }  du,\  | x | < \infty .
 
−
$$
 
  
−
In particular, if $  f= 1 $,  
+
In particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071014.png" />, then
−
then
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071015.png" /></td> </tr></table>
−
S _ {1} ( x)  =
 
−
\frac{1}{2}
 
−
+
 
−
\frac{1} \pi
 
−
  \mathop{\rm arctan}  x
 
−
$$
 
  
 
is the distribution function of the [[Cauchy distribution|Cauchy distribution]]. The probability density of the Student distribution is symmetric about 0, therefore
 
is the distribution function of the [[Cauchy distribution|Cauchy distribution]]. The probability density of the Student distribution is symmetric about 0, therefore
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071016.png" /></td> </tr></table>
−
S _ {f} ( t) + S _ {f} (- t)  = 1
 
−
\  \textrm{ for  any  }  t \in \mathbf R  ^ {1} .
 
−
$$
 
−
 
 
−
The moments  $  \mu _ {r} = {\mathsf E} t _ {f}  ^ {r} $
 
−
of a Student distribution exist only for  $  r < f $,
 
−
the odd moments are equal to 0, and, in particular  $  {\mathsf E} t _ {f} = 0 $.  
 
−
The even moments of a Student distribution are expressed by the formula
 
−
 
 
−
$$
 
−
\mu _ {2r}  =  f ^ { r }
 
−
\frac{\Gamma ( ( r + 1 ) / 2 ) \Gamma
 
−
( f / 2 - r ) }{\sqrt \pi \Gamma ( f / 2 ) }
 
−
,\ \
 
−
2 \leq  2r < f  ;
 
−
$$
 
−
 
 
−
in particular,  $  \mu _ {2} = {\mathsf D} \{ t _ {f} \} = f/( f- 2) $.
 
−
The distribution function  $  S _ {f} ( x) $
 
−
of the random variable  $  t _ {f} $
 
−
is expressed in terms of the [[Beta-distribution|beta-distribution]] function in the following way:
 
−
 
 
−
$$
 
−
S _ {f} ( x)  =  1 -
 
−
\frac{1}{2}
 
−
I _ {f/( f+ x  ^ {2}  ) } \left (
 
−
\frac{f}{2}
 
−
,
 
−
\frac{1}{2}
 
−
 
 
−
\right ) ,
 
−
$$
 
  
−
where  $  I _ {z} ( a, b) $
+
The moments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071017.png" /> of a Student distribution exist only for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071018.png" />, the odd moments are equal to 0, and, in particular <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071019.png" />. The even moments of a Student distribution are expressed by the formula
−
is the incomplete beta-function, $  0 \leq  z \leq  1 $.  
 
−
If  $  f \rightarrow \infty $,
 
−
then the Student distribution converges to the standard normal law, i.e.
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071020.png" /></td> </tr></table>
−
\lim\limits _ {f\rightarrow \infty }  S _ {f} ( x)  = \
 
−
\Phi ( x)  = \
 
  
−
\frac{1}{\sqrt {2 \pi } }
+
in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071021.png" />. The distribution function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071022.png" /> of the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071023.png" /> is expressed in terms of the [[Beta-distribution|beta-distribution]] function in the following way:
−
\int\limits _ {- \infty } ^ { x }  e ^ {- t  ^ {2} /2 }  dt.
 
−
$$
 
  
−
Example. Let  $  X _ {1} \dots X _ {n} $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071024.png" /></td> </tr></table>
−
be independent, identically, normally  $  N( a, \sigma  ^ {2} ) $-
 
−
distributed random variables, where the parameters  $  a $
 
−
and  $  \sigma  ^ {2} $
 
−
are unknown. Then the statistics
 
  
−
$$
+
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071025.png" /> is the incomplete beta-function, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071026.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071027.png" />, then the Student distribution converges to the standard normal law, i.e.
−
\overline{X}\;  =
 
−
\frac{1}{n}
 
−
\sum _ { i= } 1 ^ { n }  X _ {i} \  \textrm{ and } \ \
 
−
s ^ {2}  =
 
−
\frac{1}{n-}
 
−
1 \sum _ { i= } 1 ^ { n }  ( X _ {i} - \overline{X}\; )  ^ {2}
 
−
$$
 
  
−
are the best unbiased estimators of  $  a $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071028.png" /></td> </tr></table>
−
and  $  \sigma  ^ {2} $;  
 
−
here  $  \overline{X}\; $
 
−
and  $  s ^ {2} $
 
−
are stochastically independent. Since the random variable  $  \sqrt n ( \overline{X}\; - a)/ \sigma $
 
−
is subject to the standard normal law, while
 
  
−
$$
+
Example. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071029.png" /> be independent, identically, normally <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071030.png" />-distributed random variables, where the parameters <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071031.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071032.png" /> are unknown. Then the statistics
−
n-  
 
−
\frac{1}{\sigma  ^ {2} }
 
−
s ^ {2}  = \chi _ {n-} 1  ^ {2}
 
−
$$
 
  
−
is distributed according to the  "chi-squared" law with  $  f= n- 1 $
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071033.png" /></td> </tr></table>
−
degrees of freedom, then by virtue of their independence, the fraction
 
  
−
$$
+
are the best unbiased estimators of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071034.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071035.png" />; here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071036.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071037.png" /> are stochastically independent. Since the random variable <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071038.png" /> is subject to the standard normal law, while
  
−
\frac{\sqrt n ( \overline{X}\; - a) / \sigma }{\sqrt {\chi _ {n-} 1  ^ {2} / ( n- 1) } }
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071039.png" /></td> </tr></table>
  
−
  =
+
is distributed according to the "chi-squared"  law with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071040.png" /> degrees of freedom, then by virtue of their independence, the fraction
−
\frac{\sqrt n ( \overline{X}\; - a) }{s}
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071041.png" /></td> </tr></table>
  
−
is subject to the Student distribution with $  f= n- 1 $
+
is subject to the Student distribution with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071042.png" /> degrees of freedom. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071043.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071044.png" /> be the solutions of the equations
−
degrees of freedom. Let $  t _ {f} ( P) $
 
−
and $  t _ {f} ( 1- P) = - t _ {f} ( P) $
 
−
be the solutions of the equations
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071045.png" /></td> </tr></table>
−
S _ {n-} 1 \left (
 
−
\frac{\sqrt n ( \overline{X}\; - a) }{s}
 
−
\right )  = \
 
−
\left \{
 
  
−
Then the statistics $  \overline{X}\; - ( s/ \sqrt n ) t _ {f} ( P) $
+
Then the statistics <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071046.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071047.png" /> are the lower and upper bounds of the confidence set for the unknown mathematical expectation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071048.png" /> of the normal law <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071049.png" />, and the confidence coefficient of this confidence set is equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071050.png" />, i.e.
−
and $  \overline{X}\; + ( s/ \sqrt n ) t _ {f} ( P) $
 
−
are the lower and upper bounds of the confidence set for the unknown mathematical expectation $  a $
 
−
of the normal law $  N( a, \sigma  ^ {2} ) $,
 
−
and the confidence coefficient of this confidence set is equal to $  2P- 1 $,  
 
−
i.e.
 
  
−
$$
+
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090710/s09071051.png" /></td> </tr></table>
−
{\mathsf P} \left \{ \overline{X}\; -
 
−
\frac{s}{\sqrt n }
 
−
t _ {f} ( P) < a < \overline{X}\; +
 
−
\frac{s}{\sqrt
 
−
n }
 
−
t _ {f} ( P) \right \}  =  2P- 1.
 
−
$$
 
  
 
The Student distribution was first used by W.S. Gosset (pseudonym Student).
 
The Student distribution was first used by W.S. Gosset (pseudonym Student).

Revision as of 14:53, 7 June 2020

with degrees of freedom, 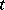-distribution

The probability distribution of the random variable

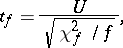where 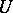is a random variable subject to the standard normal law 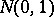and 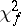is a random variable not depending on 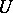and subject to the "chi-squared" distribution with 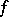degrees of freedom. The distribution function of the random variable 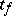is expressed by the formula

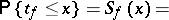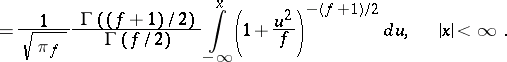In particular, if 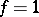, then

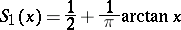is the distribution function of the Cauchy distribution. The probability density of the Student distribution is symmetric about 0, therefore

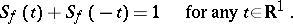The moments 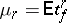of a Student distribution exist only for 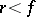, the odd moments are equal to 0, and, in particular 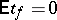. The even moments of a Student distribution are expressed by the formula

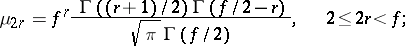in particular, 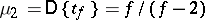. The distribution function 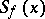of the random variable 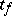is expressed in terms of the beta-distribution function in the following way:

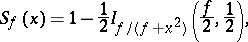where is the incomplete beta-function, 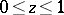. If 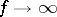, then the Student distribution converges to the standard normal law, i.e.

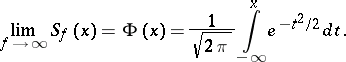Example. Let be independent, identically, normally 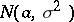-distributed random variables, where the parameters and 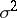are unknown. Then the statistics

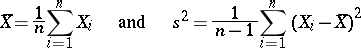are the best unbiased estimators of and 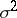; here 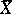and 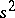are stochastically independent. Since the random variable is subject to the standard normal law, while

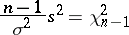is distributed according to the "chi-squared" law with degrees of freedom, then by virtue of their independence, the fraction

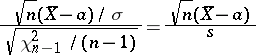is subject to the Student distribution with 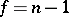degrees of freedom. Let 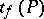and 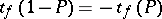be the solutions of the equations

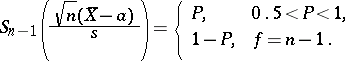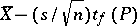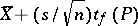Then the statistics and are the lower and upper bounds of the confidence set for the unknown mathematical expectation of the normal law 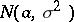, and the confidence coefficient of this confidence set is equal to 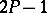, i.e.

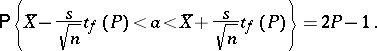The Student distribution was first used by W.S. Gosset (pseudonym Student).

References

[1] H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946)
[2] L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova)
[3] "Student" (W.S. Gosset), "The probable error of a mean" Biometrika , 6 (1908) pp. 1–25
How to Cite This Entry:
Student distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Student_distribution&oldid=48882
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Student_distribution&oldid=49453"