Structure space
of a ring
The set  of all its primitive ideals with the following topology: A subset
of all its primitive ideals with the following topology: A subset  is closed if
is closed if 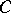 contains every ideal that contains the intersection of all ideals from
contains every ideal that contains the intersection of all ideals from 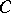 (see Zariski topology). The structure space of a ring
(see Zariski topology). The structure space of a ring 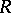 is homeomorphic to the structure space of the quotient ring
is homeomorphic to the structure space of the quotient ring 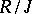 , where
, where 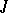 is the Jacobson radical. A structure space is a
is the Jacobson radical. A structure space is a 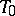 -space; if all primitive ideals of the ring are maximal, then the structure space is a
-space; if all primitive ideals of the ring are maximal, then the structure space is a 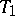 -space. The structure space of a ring with a unit is compact. The structure space of a biregular ring (see Regular ring (in the sense of von Neumann)) is locally compact and totally disconnected. It is used to represent a biregular ring in the form of a ring of continuous functions with compact supports.
-space. The structure space of a ring with a unit is compact. The structure space of a biregular ring (see Regular ring (in the sense of von Neumann)) is locally compact and totally disconnected. It is used to represent a biregular ring in the form of a ring of continuous functions with compact supports.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
Comments
This is an extension of the notion of the spectrum space of maximal ideals of a commutative ring (cf. Spectrum of a ring).
References
| [a1] | K.R. Goodearl, "Von Neumann regular rings" , Pitman (1979) |
Structure space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Structure_space&oldid=12816