Structure(2)
Also called mathematical structure. A generic name for unifying concepts whose general characteristic is that they can be applied to sets whose elements are of an indefinite nature. In order to define a structure, relations are given in which the elements of the set appear (the type characteristic of a structure), and it is then postulated that these relations satisfy certain conditions — axioms of the structure.
References
| [1] | N. Bourbaki, "Eléments d'histoire des mathématiques" , Hermann (1960) |
| [2] | N. Bourbaki, "Elements of mathematics. Theory of sets" , Addison-Wesley (1968) (Translated from French) |
Comments
Sets endowed with a given structure plus mappings of sets which preserve this structure together form a category. Such categories are called concrete (cf. also Category; Sets, category of). More precisely, a concrete category is a pair 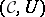 consisting of a category
consisting of a category 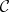 and a faithful functor
and a faithful functor 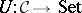 . Because
. Because 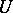 is faithful,
is faithful, 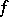 can be identified with
can be identified with 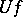 , and an object
, and an object 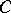 of a concrete category is a set
of a concrete category is a set 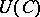 with extra structure while a morphism
with extra structure while a morphism 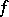 is an actual mapping of sets that preserves the extra structure; composition of morphisms is accomplished by the usual composition of mappings of sets. Often the set of morphisms
is an actual mapping of sets that preserves the extra structure; composition of morphisms is accomplished by the usual composition of mappings of sets. Often the set of morphisms 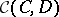 consists of all structure-preserving mappings of sets, but this need not be the case.
consists of all structure-preserving mappings of sets, but this need not be the case.
A category is concrete if and only if it satisfies the Isbell condition (the Freyd concreteness theorem). Here, the Isbell condition is the following. A span in a category is a diagram of the form
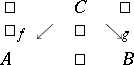 |
Two  -spans
-spans 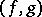 and
and 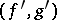 are equivalent if for all pairs of morphisms
are equivalent if for all pairs of morphisms 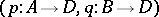 either both diagrams
either both diagrams
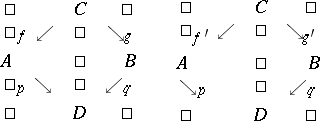 |
commute or both do not commute. A category satisfies the Isbell condition if for all objects 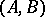 there exists a set of
there exists a set of 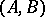 -spans
-spans 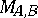 such that each
such that each 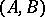 -span is equivalent to precisely one element of
-span is equivalent to precisely one element of 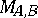 .
.
References
| [a1] | J. Adamek, "Theory of mathematical structures" , Reidel (1983) pp. Chapt. 6 |
| [a2] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. 26 |
A structure is also an obsolete term for lattice.
Comments
References
| [a1] | A.G. Kurosh, "Theory of groups" , 2 , Chelsea, reprint (1955) pp. 85 (Translated from Russian) |
A structure on a manifold, a geometric quantity, a geometric object, or a field of geometric objects, is a section of a bundle associated with the principal bundle of coframes on the manifold 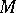 . Intuitively, a geometric quantity can be considered as a quantity whose value depends not only on the point
. Intuitively, a geometric quantity can be considered as a quantity whose value depends not only on the point  of the manifold
of the manifold  , but also on the choice of the coframe — an infinitesimal system of coordinates at the point
, but also on the choice of the coframe — an infinitesimal system of coordinates at the point  (see Chart).
(see Chart).
More precisely, let 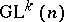 be the general differential group of order
be the general differential group of order 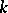 (the group of
(the group of 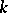 -jets at zero of transformations of the space
-jets at zero of transformations of the space 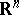 that preserve the origin), and let
that preserve the origin), and let 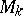 be the manifold of coframes of order
be the manifold of coframes of order 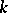 of an
of an  -dimensional manifold
-dimensional manifold 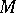 (i.e. the manifold of
(i.e. the manifold of 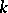 -jets
-jets 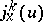 of local charts
of local charts 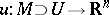 with origin at the point
with origin at the point 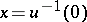 ). The group
). The group 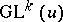 acts from the left on
acts from the left on 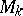 by
by
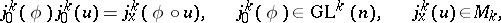 |
and this action defines on 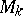 the structure of a principal
the structure of a principal 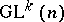 -bundle
-bundle 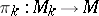 , which is called the bundle of coframes of order
, which is called the bundle of coframes of order 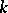 . Let
. Let 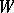 be an arbitrary
be an arbitrary 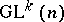 -manifold, i.e. a manifold with a left action of the group
-manifold, i.e. a manifold with a left action of the group  . Finally, let
. Finally, let 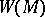 be the orbit space of the left action of
be the orbit space of the left action of 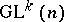 on
on 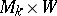 , while
, while 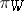 is its natural projection onto
is its natural projection onto 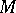 . The bundle
. The bundle  (associated with
(associated with 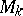 and
and 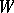 ) is called a bundle of geometric structures of order
) is called a bundle of geometric structures of order 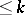 and of type
and of type 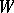 , while its sections are called structures of type
, while its sections are called structures of type 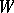 . Structures of type
. Structures of type  are in a natural one-to-one correspondence with
are in a natural one-to-one correspondence with 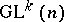 -equivariant mappings
-equivariant mappings 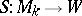 . Thus, a structure of type
. Thus, a structure of type 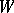 can be seen as a
can be seen as a 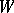 -valued function
-valued function 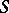 on the manifold
on the manifold 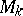 of
of 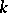 -frames that satisfies the following condition of equivariance:
-frames that satisfies the following condition of equivariance:
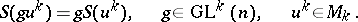 |
The bundle  of geometric objects is a natural bundle in the sense that the diffeomorphism group of
of geometric objects is a natural bundle in the sense that the diffeomorphism group of 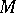 acts as the automorphism group of
acts as the automorphism group of 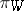 .
.
If 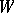 is a vector space with a linear (or affine) action of
is a vector space with a linear (or affine) action of 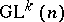 , then a structure of type
, then a structure of type 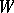 is said to be linear (or affine).
is said to be linear (or affine).
A basic example of a linear structure of order one is a tensor structure, or a tensor field. Let 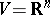 ,
,  and let
and let  be the space of tensors of type
be the space of tensors of type 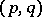 with the natural tensor representation of
with the natural tensor representation of 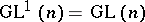 . A structure of type
. A structure of type 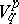 is called a tensor field of type
is called a tensor field of type 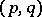 . It can be regarded as a vector function on the manifold of coframes
. It can be regarded as a vector function on the manifold of coframes 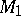 which assigns to the coframe
which assigns to the coframe 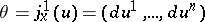 the set of coordinates
the set of coordinates 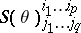 of the tensor
of the tensor 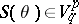 , relative to the standard basis
, relative to the standard basis
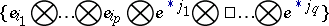 |
of 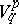 . Given a linear transformation of coframes
. Given a linear transformation of coframes 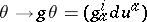 , the coordinates
, the coordinates 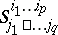 are transformed in accordance with the tensor representation:
are transformed in accordance with the tensor representation:
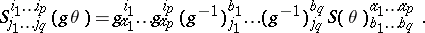 |
The most important examples of tensor structures are a vector field, a Riemannian metric, a differential form, a symplectic structure, a complex structure, and most commonly, an affinor. All linear structures (of whatever order) are exhausted by Rashevskii super-tensors (see [4]). An example of an affine structure of order two is an affine connection without torsion, which can be regarded as a structure of type 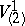 , where
, where 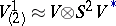 is the kernel of the natural homomorphism
is the kernel of the natural homomorphism 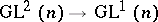 , considered as a vector space with the natural action of
, considered as a vector space with the natural action of 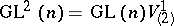 . A large and important class of structures is the class of infinitesimally-homogeneous structures or
. A large and important class of structures is the class of infinitesimally-homogeneous structures or 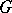 -structures (cf.
-structures (cf. 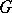 -structure) — structures of type
-structure) — structures of type 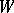 , where
, where 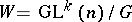 is a homogeneous space of the group
is a homogeneous space of the group 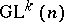 .
.
The above definition of a structure is not sufficiently general, and does not include a number of important geometric structures such as a spinor structure, a symplectic spinor structure, etc. A natural generalization is to study generalized  -structures that are principal bundles with a fixed homomorphism onto a
-structures that are principal bundles with a fixed homomorphism onto a 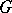 -structure, and sections of associated bundles.
-structure, and sections of associated bundles.
References
| [1] | P. Rashevskii, "Caractères tensoriels de l'espace sousprojectif" Trudy Sem. Vektor. i Tenzor. Anal. , 1 (1933) pp. 126–142 |
| [2] | V. Vagner, "The theory of geometric objects and the theory of finite and infinite continuous transformation groups" Dokl. Akad. Nauk SSSR , 46 : 9 (1945) pp. 347–349 (In Russian) |
| [3] | O. Veblen, J.H.C. Whitehead, "The foundations of differential geometry" , Cambridge Univ. Press (1932) |
| [4] | P.K. Rashevskii, "On linear representations of differential groups and Lie groups with nilpotent radical" Trudy Moskov. Mat. Obshch. , 6 (1957) pp. 337–370 (In Russian) |
| [5] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
| [6] | Ch. Ehresmann, "Introduction à la théorie des structures infinitésimals et des pseudo-groupes de Lie" , Géométrie Diff. Coll. Internat. C.N.R.S. (1953) pp. 97–110 |
D.V. Alekseevskii
Comments
Historically, E. Cartan was the first to introduce the concept of a structure.
References
| [a1] | E. Cartan, "La théorie des groupes et les récherches récentes de géometrie différentielle" Enseign. Math. , 24 (1925) pp. 5–18 |
Structure(2). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Structure(2)&oldid=14469