Strophoid
From Encyclopedia of Mathematics
The printable version is no longer supported and may have rendering errors. Please update your browser bookmarks and please use the default browser print function instead.
A third-order plane algebraic curve whose equation takes the form
$$y^2=x^2\frac{d+x}{d-x}$$
in Cartesian coordinates, and
$$\rho=-d\frac{\cos2\phi}{\cos\phi}$$
in polar coordinates. The coordinate origin is a node with tangents $y=\pm x$ (see Fig.). The asymptote is $x=d$. The area of the loop is
$$S=2d^2-\frac{1}{2\pi d^2}.$$
The area between the curve and the asymptote is
$$S_2=2d^2+\frac{1}{2\pi d^2}.$$
A strophoid is related to the so-called cusps (cf. Cusp).
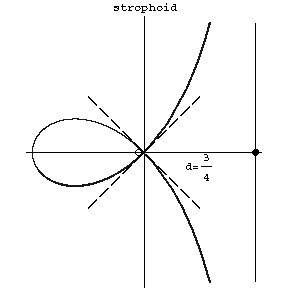
Figure: s090630a
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
| [2] | A.S. Smogorzhevskii, E.S. Stolova, "Handbook of the theory of planar curves of the third order" , Moscow (1961) (In Russian) |
| [a1] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
| [a2] | J.D. Lawrence, "A catalog of special planar curves" , Dover, reprint (1972) |
🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️
How to Cite This Entry:
Strophoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strophoid&oldid=53713
Strophoid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strophoid&oldid=53713
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article