Strongly countably complete topological space
A topological space  for which there is a sequence
for which there is a sequence  of open coverings of
of open coverings of  such that a sequence
such that a sequence  of closed subsets of
of closed subsets of  has a non-empty intersection whenever
has a non-empty intersection whenever  for all
for all  and each
and each  is a subset of some member of
is a subset of some member of  .
.
Locally countably compact spaces and Čech-complete spaces are strongly countably complete. Every strongly countably complete space is a Baire space (but not vice versa).
This rather technical notion plays an important role in questions whether separate continuity of a mapping on a product  implies joint continuity on a large subset of
implies joint continuity on a large subset of 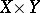 , see Namioka space; Namioka theorem; Separate and joint continuity; or [a2].
, see Namioka space; Namioka theorem; Separate and joint continuity; or [a2].
Strongly countably complete topological spaces were introduced by Z. Frolík, [a1].
References
| [a1] | Z. Frolík, "Baire spaces and some generalizations of complete metric spaces" Czech. Math. J. , 11 (1961) pp. 237–248 |
| [a2] | I. Namioka, "Separate continuity and joint continuity" Pacific J. Math. , 51 (1974) pp. 515–531 |
Strongly countably complete topological space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strongly_countably_complete_topological_space&oldid=17711