Strongly-continuous semi-group
A family 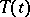 ,
,  , of bounded linear operators on a Banach space
, of bounded linear operators on a Banach space 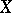 with the following properties:
with the following properties:
1) 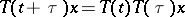 ,
, 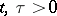 ,
, 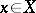 ;
;
2) the function 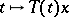 is continuous on
is continuous on 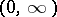 for any
for any  .
.
When 1) holds, the measurability of all functions 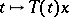 ,
, 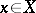 , and, in particular, their one-sided (right or left) weak continuity, implies strong continuity of
, and, in particular, their one-sided (right or left) weak continuity, implies strong continuity of 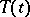 . For a strongly-continuous semi-group the finite number
. For a strongly-continuous semi-group the finite number
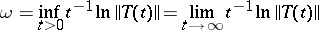 |
is called the type of the semi-group. Thus, the norms of the functions 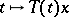 grow at
grow at 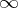 no faster than the exponential
no faster than the exponential 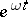 . The classification of strongly-continuous semi-groups is based on their behaviour as
. The classification of strongly-continuous semi-groups is based on their behaviour as 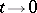 . If there is a bounded operator
. If there is a bounded operator 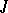 such that
such that 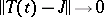 as
as 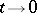 , then
, then  is a projection operator and
is a projection operator and 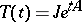 , where
, where 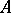 is a bounded linear operator commuting with
is a bounded linear operator commuting with 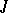 . In this case
. In this case 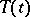 is continuous with respect to the operator norm. If
is continuous with respect to the operator norm. If 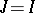 , then
, then 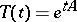 ,
, 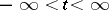 , is a uniformly-continuous group of operators.
, is a uniformly-continuous group of operators.
If 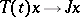 for each
for each 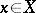 , then
, then  is also a projection operator, projecting
is also a projection operator, projecting 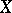 onto the subspace
onto the subspace 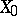 that is the closure of the union of all
that is the closure of the union of all 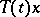 ,
, 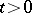 ,
, 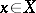 .
.
For 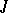 to exist and to be equal to
to exist and to be equal to 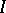 it is necessary and sufficient that
it is necessary and sufficient that 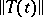 be bounded on
be bounded on 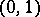 and that
and that  . In this case the semi-group
. In this case the semi-group 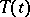 can be extended by the equality
can be extended by the equality 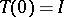 and is strongly continuous for
and is strongly continuous for 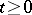 (it satisfies the
(it satisfies the  -condition). For broader classes of semi-groups the limit relation
-condition). For broader classes of semi-groups the limit relation 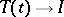 is satisfied in a generalized sense:
is satisfied in a generalized sense:
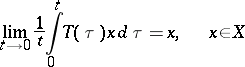 |
(Cesáro summability, the  -condition), or
-condition), or
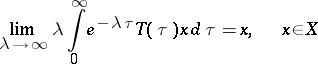 |
(Abel summability, the 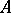 -condition). Here it is assumed that the function
-condition). Here it is assumed that the function 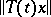 ,
, 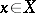 , is integrable on
, is integrable on 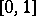 (and, hence, on any finite interval).
(and, hence, on any finite interval).
The behaviour of a strongly-continuous semi-group as  can be completely irregular. For example, the function
can be completely irregular. For example, the function 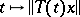 may have a power singularity at
may have a power singularity at 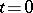 .
.
For a dense set of  in
in  the function
the function 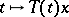 is differentiable on
is differentiable on 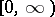 . An important role is played by strongly-continuous semi-groups for which the function
. An important role is played by strongly-continuous semi-groups for which the function 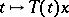 is differentiable for all
is differentiable for all  for
for 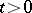 . In this case the operator
. In this case the operator 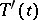 is bounded for each
is bounded for each 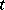 and its behaviour as
and its behaviour as 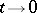 gives new opportunities for classifying semi-groups. The classes of strongly-continuous semi-groups for which
gives new opportunities for classifying semi-groups. The classes of strongly-continuous semi-groups for which 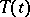 admits a holomorphic extension in a sector of the complex plane containing the semi-axis
admits a holomorphic extension in a sector of the complex plane containing the semi-axis 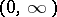 have been characterized.
have been characterized.
See Semi-group of operators; Generating operator of a semi-group.
References
| [1] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) |
Comments
References
| [a1] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) |
| [a2] | W. Arendt, A. Grabosch, G. Greiner, U. Groh, H.P. Lotz, U. Moustakas, R. Nagel, F. Neubrander, U. Schlotterbeck, "One parameter semigroups of positive operators" , Lect. notes in math. , 1184 , Springer (1986) |
| [a3] | Yu.I. [Yu.I. Daletskii] Daleckii, "Stability of solutions of differential equations in Banach space" , Amer. Math. Soc. (1974) (Translated from Russian) |
Strongly-continuous semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strongly-continuous_semi-group&oldid=19003