Strong solution
From Encyclopedia of Mathematics
of a differential equation
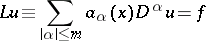 |
in a domain 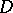
A locally integrable function  that has locally integrable generalized derivatives of all orders
that has locally integrable generalized derivatives of all orders  (cf. Generalized derivative), and satisfies
(cf. Generalized derivative), and satisfies
almost-everywhere in 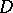 .
.
The notion of a "strong solution" can also be introduced as follows. A function  is called a strong solution of
is called a strong solution of
if there are sequences of smooth (for example,  ) functions
) functions 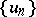 ,
, 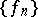 such that
such that 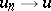 ,
, 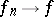 and
and 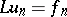 for each
for each  , where the convergence is taken in
, where the convergence is taken in 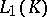 for any compact set
for any compact set 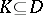 . In these definitions,
. In these definitions, 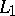 can be replaced by the class
can be replaced by the class 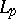 of functions whose
of functions whose 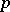 -th powers are locally integrable. The class most often used is
-th powers are locally integrable. The class most often used is 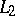 .
.
In the case of an elliptic equation
both notions of a strong solution coincide.
Comments
References
| [a1] | J. Chazarain, A. Piriou, "Introduction à la théorie des équations aux dérivées partielles linéaires" , Gauthier-Villars (1981) pp. 223 |
How to Cite This Entry:
Strong solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_solution&oldid=16232
Strong solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_solution&oldid=16232
This article was adapted from an original article by A.P. Soldatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article