Difference between revisions of "Strong solution"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 23: | Line 23: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Chazarain, A. Piriou, "Introduction à la théorie des équations aux dérivées partielles linéaires" , Gauthier-Villars (1981) pp. 223</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Chazarain, A. Piriou, "Introduction à la théorie des équations aux dérivées partielles linéaires" , Gauthier-Villars (1981) pp. 223 {{MR|0598467}} {{ZBL|0446.35001}} </TD></TR></table> |
Revision as of 12:13, 27 September 2012
of a differential equation
 |
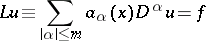in a domain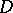 
A locally integrable function 
that has locally integrable generalized derivatives of all orders 
(cf. Generalized derivative), and satisfies
almost-everywhere in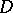 
.
The notion of a "strong solution" can also be introduced as follows. A function 
is called a strong solution of
if there are sequences of smooth (for example, 
) functions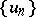 
, 
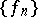such that 
, 
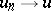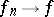and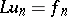 
for each 
, where the convergence is taken in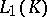 
for any compact set 
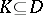. In these definitions, 
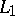can be replaced by the class 
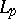of functions whose 
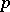-th powers are locally integrable. The class most often used is 
.
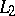In the case of an elliptic equation
both notions of a strong solution coincide.
Comments
References
| [a1] | J. Chazarain, A. Piriou, "Introduction à la théorie des équations aux dérivées partielles linéaires" , Gauthier-Villars (1981) pp. 223 MR0598467 Zbl 0446.35001 |
How to Cite This Entry:
Strong solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_solution&oldid=16232
Strong solution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_solution&oldid=16232
This article was adapted from an original article by A.P. Soldatov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article