Difference between revisions of "Strong Stieltjes moment problem"
(Importing text file) |
m (AUTOMATIC EDIT (latexlist): Replaced 54 formulas out of 58 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| − | + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | |
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| − | + | Out of 58 formulas, 54 were replaced by TEX code.--> | |
| − | + | {{TEX|semi-auto}}{{TEX|partial}} | |
| + | The strong Stieltjes moment problem for a given sequence $\{ c _ { n } \} _ { n = - \infty } ^ { \infty }$ of real numbers is concerned with finding real-valued, bounded, monotone non-decreasing functions $\psi ( t )$ with infinitely many points of increase for $0 \leq t < \infty$ such that | ||
| − | + | \begin{equation} \tag{a1} c _ { n } = \int _ { 0 } ^ { \infty } t ^ { n } d \psi ( t ) ,\; n = 0 , \pm 1 , \pm 2, \dots . \end{equation} | |
| − | + | This problem, which generalizes the classical Stieltjes moment problem (where the given sequence is $\{ c _ { n } \} _ { n = 0 } ^ { \infty }$; cf. also [[Krein condition|Krein condition]]), was first studied by W.B. Jones, W.J. Thron and H. Waadeland [[#References|[a1]]]. | |
| − | + | Let $\Lambda _ { p , q }$ be the complex linear space spanned by the set of functions $\{ z ^ { j } \} _ { j = p } ^ { q }$ with $p \leq q$, and define $\Lambda _ { 2 m } = \Lambda - m , m$ and $\Lambda _ { 2 m + 1 } = \Lambda_{ - ( m + 1 ) , m}$ for $m = 0,1 , \ldots$, and $\Lambda = \cup _ { n = 0 } ^ { \infty } \Lambda _ { n }$. An element of $\Lambda$ is called a Laurent polynomial. For a given sequence $\{ c _ { n } \} _ { n = - \infty } ^ { \infty }$, a necessary and sufficient condition for the strong Stieltjes moment problem to be solvable is that the [[Linear operator|linear operator]] $M$ defined on the base elements $z ^ { n }$ of $\Lambda$ by | |
| − | + | \begin{equation} \tag{a2} M [ z ^ { n } ] = c _ { n } , n = 0 , \pm 1 , \pm 2 , \dots, \end{equation} | |
| − | + | is positive on $( 0 , \infty )$, i.e. for any $L \in \Lambda$ such that $L ( z ) \geq 0$ for $z \in ( 0 , \infty )$ and $L ( z ) \not\equiv 0$, then $M [ L ] > 0$. An equivalent condition is that if | |
| − | + | \begin{equation} \tag{a3} H _ { 0 } ^ { ( m ) } = 1 ,\, H _ { k } ^ { ( m ) } = \operatorname { det } ( c_{ m + i + j} ) _ { i ,\, j = 0 } ^ { k - 1 } \end{equation} | |
| − | + | for $m = 0 , \pm 1 , \pm 2 , \dots$, $k = 1,2 , \dots$, are the Hankel determinants associated with $\{ c _ { k } \}$ (cf. also [[Hankel matrix|Hankel matrix]]), then | |
| − | + | \begin{equation*} H _ { k } ^ { ( m ) } > 0 , m = 0 , \pm 1 , \pm 2 , \ldots , k = 1,2 ,\dots . \end{equation*} | |
| − | + | Orthogonal Laurent polynomials $\{ Q _ { n } ( z ) \in \Lambda _ { n } : n = 0,1 , \ldots \}$ may be defined with respect to the [[Inner product|inner product]] $\langle P , Q \rangle \equiv M [ P ( z ) Q ( z ) ]$ and are given by: | |
| + | |||
| + | \begin{equation} \tag{a4} Q _ { 2 n } ( z ) = \frac { 1 } { H _ { 2 n } ^ { ( - 2 n ) } } \left| \begin{array} { c c c c } { c _ { - 2 n } } & { \cdots } & { c _ { - 1 } } & { z ^ { - n } } \\ { \vdots } & { \square } & { \vdots } & { \vdots } \\ { c _ { - 1 } } & { \cdots } & { c _ { 2 n - 2 } } & { z ^ { n - 1 } } \\ { c_0 } & { \cdots } & { c _ { 2 n - 1 } } & { z ^ { n } e n d } \end{array} \right|, \end{equation} | ||
| + | |||
| + | \begin{equation*} n = 1,2 , \dots , \end{equation*} | ||
and | and | ||
| − | + | \begin{equation} \tag{a5} Q _ { 2 n + 1 } ( z ) = \frac { - 1 } { H _ { 2 n + 1 } ^ { ( - 2 n ) } } \left| \begin{array} { c c c c } { c_{ - 2 n - 1} } & { \cdots } & { c_{ - 1} } & { z ^ { - n - 1 } } \\ { \vdots } & { \square } & { \vdots } & { \vdots } \\ { c_{ - 1} } & { \cdots } & { c _ { 2 n - 1 } } & { z ^ { n - 1 } } \\ { c_0 } & { \cdots } & { c _ { 2 n } } & { z ^ { n } e n d } \end{array} \right|, \end{equation} | |
| − | + | \begin{equation*} n = 0,1 , \ldots , \end{equation*} | |
| − | and | + | and $Q _ { 0 } ( z ) = 1$. Corresponding associated orthogonal Laurent polynomials $\{ P _ { n } \}$ are defined by |
| − | + | \begin{equation} \tag{a6} P _ { n } = M \left[ \frac { Q _ { n } ( t ) - Q _ { n } ( z ) } { t - z } \right] , n = 0,1 ,\dots . \end{equation} | |
| − | The rational functions | + | The rational functions $( - z ) P _ { n } ( - z ) / Q _ { n } ( - z )$ are the convergents of the positive T-fraction [[#References|[a3]]], |
| − | + | \begin{equation} \tag{a7} \frac { F _ { 1 } z } { 1 + G _ { 1 } z } \square _ { + } \frac { F _ { 2 } z } { 1 + G _ { 2 } z } \square _ { + } \frac { F _ { 3 } } { 1 + G _ { 3 } z } \square _ { + } \dots \end{equation} | |
| − | + | \begin{equation*} ( F _ { n } > 0 , G _ { n } > 0 ), \end{equation*} | |
where | where | ||
| − | + | \begin{equation*} F _ { n } = \frac { H _ { n } ^ { ( - n ) } H _ { n-2 } ^ { ( - n + 3 ) } } { H _ { n-1 } ^ { ( - n + 2 ) } H _ { n - 1 } ^ { ( - n + 1 ) } }, \end{equation*} | |
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130590/s13059043.png"/></td> </tr></table> |
which corresponds to the formal pair of power series, | which corresponds to the formal pair of power series, | ||
| − | + | \begin{equation} \tag{a8} L _ { 0 } = - \sum _ { k = 1 } ^ { \infty } c _ { - k } ( - z ) ^ { k } , L _ { \infty } = \sum _ { k = 0 } ^ { \infty } c _ { k } ( - z ) ^ { - k }. \end{equation} | |
The T-fraction is equivalent to the [[Continued fraction|continued fraction]] | The T-fraction is equivalent to the [[Continued fraction|continued fraction]] | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s130/s130590/s13059045.png"/></td> <td style="width:5%;text-align:right;" valign="top">(a9)</td></tr></table> |
where | where | ||
| − | + | \begin{equation} \tag{a10} F _ { n } = \frac { 1 } { e _ { n } e _ { n - 1} } ,\, G _ { n } = \frac { d _ { n } } { e _ { n } } ( e_{ 0} = 1 ), \end{equation} | |
| − | + | \begin{equation*} n = 1,2 , \dots \end{equation*} | |
| − | The following result may then be proved [[#References|[a1]]]: The solution of the strong Stieltjes moment problem (a1) is unique if and only if at least one of the series | + | The following result may then be proved [[#References|[a1]]]: The solution of the strong Stieltjes moment problem (a1) is unique if and only if at least one of the series $\sum e_{ n}$, $\sum d _ { n }$ diverges, and then |
| − | + | \begin{equation} \tag{a11} \operatorname { lim } _ { n \rightarrow \infty } \left[ ( - z ) \frac { P _ { n } ( - z ) } { Q _ { n } ( - z ) } \right] = z \int _ { 0 } ^ { \infty } \frac { d \psi ( t ) } { z + t }, \end{equation} | |
| − | where | + | where $\psi ( t )$ is this unique solution.The convergence is uniform on every compact subset of $R = \{ z : | \operatorname { arg } z | < \pi \}$. |
The strong Stieltjes moment problem is said to be determinate when it has a unique solution and indeterminate otherwise. A detailed discussion of the latter case has been given in [[#References|[a4]]]. | The strong Stieltjes moment problem is said to be determinate when it has a unique solution and indeterminate otherwise. A detailed discussion of the latter case has been given in [[#References|[a4]]]. | ||
| Line 69: | Line 77: | ||
A classic example of a strong Stieltjes moment problem is the log-normal distribution, | A classic example of a strong Stieltjes moment problem is the log-normal distribution, | ||
| − | + | \begin{equation*} \frac { d \psi ( t ) } { d t } = \frac { q ^ { 1 / 2 } } { 2 \kappa \sqrt { \pi } } e ^ { - ( \operatorname { ln } t / 2 \kappa ) ^ { 2 } } ,\, q = e ^ { - 2 \kappa ^ { 2 } }. \end{equation*} | |
| − | (Cf. also [[Normal distribution|Normal distribution]].) The corresponding sequence of moments is | + | (Cf. also [[Normal distribution|Normal distribution]].) The corresponding sequence of moments is $\{ c _ { n } \}$, where |
| − | + | \begin{equation*} c _ { n } = q ^ { - n - n ^ { 2 } / 2 } , n = 0 , \pm 1 , \pm 2 , \ldots , \end{equation*} | |
and the strong Stieltjes moment problem in this case is indeterminate [[#References|[a5]]]. The moments corresponding to the log-normal distribution are related to a subclass of strong Stieltjes moment problems where | and the strong Stieltjes moment problem in this case is indeterminate [[#References|[a5]]]. The moments corresponding to the log-normal distribution are related to a subclass of strong Stieltjes moment problems where | ||
| − | + | \begin{equation*} c _ { - n } = c _ { n } , \quad n = 1,2 , \dots . \end{equation*} | |
This subclass has been called strong symmetric Stieltjes moment problems by A.K. Common and J. McCabe, who studied properties of the related continued fractions [[#References|[a6]]]. Other subclasses have been investigated in [[#References|[a7]]]. | This subclass has been called strong symmetric Stieltjes moment problems by A.K. Common and J. McCabe, who studied properties of the related continued fractions [[#References|[a6]]]. Other subclasses have been investigated in [[#References|[a7]]]. | ||
| Line 84: | Line 92: | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> W.B. Jones, O. Njåstad, W.J. Thron, "A strong Stieltjes moment problem" ''Trans. Amer. Math. Soc.'' , '''261''' (1980) pp. 503–528</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> W.B. Jones, O. Njåstad, W.J. Thron, "Continued fractions and strong Hamburger moment problems" ''Proc. London Math. Soc.'' , '''47''' (1983) pp. 105–123</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> W.B. Jones, W.J. Thron, "Continued fractions: Analytic theory and applications" , ''Encycl. Math. Appl.'' , '''11''' , Addison-Wesley (1980)</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> O. Njåstad, "Solutions of the strong Stieltjes moment problem" ''Meth. Appl. Anal.'' , '''2''' (1995) pp. 320–347</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> S.C. Cooper, W.B. Jones, W.J. Thron, "Orthogonal Laurent polynomials and continued fractions associated with log-normal distributions" ''J. Comput. Appl. Math.'' , '''32''' (1990) pp. 39–46</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> A.K. Common, J. McCabe, "The symmetric strong moment problem" ''J. Comput. Appl. Math.'' , '''67''' (1996) pp. 327–341</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> A. Sri Ranga, E.X.L. de Andrade, J. McCabe, "Some consequences of symmetry in strong distributions" ''J. Math. Anal. Appl.'' , '''193''' (1995) pp. 158–168</td></tr></table> |
Revision as of 16:57, 1 July 2020
The strong Stieltjes moment problem for a given sequence $\{ c _ { n } \} _ { n = - \infty } ^ { \infty }$ of real numbers is concerned with finding real-valued, bounded, monotone non-decreasing functions $\psi ( t )$ with infinitely many points of increase for $0 \leq t < \infty$ such that
\begin{equation} \tag{a1} c _ { n } = \int _ { 0 } ^ { \infty } t ^ { n } d \psi ( t ) ,\; n = 0 , \pm 1 , \pm 2, \dots . \end{equation}
This problem, which generalizes the classical Stieltjes moment problem (where the given sequence is $\{ c _ { n } \} _ { n = 0 } ^ { \infty }$; cf. also Krein condition), was first studied by W.B. Jones, W.J. Thron and H. Waadeland [a1].
Let $\Lambda _ { p , q }$ be the complex linear space spanned by the set of functions $\{ z ^ { j } \} _ { j = p } ^ { q }$ with $p \leq q$, and define $\Lambda _ { 2 m } = \Lambda - m , m$ and $\Lambda _ { 2 m + 1 } = \Lambda_{ - ( m + 1 ) , m}$ for $m = 0,1 , \ldots$, and $\Lambda = \cup _ { n = 0 } ^ { \infty } \Lambda _ { n }$. An element of $\Lambda$ is called a Laurent polynomial. For a given sequence $\{ c _ { n } \} _ { n = - \infty } ^ { \infty }$, a necessary and sufficient condition for the strong Stieltjes moment problem to be solvable is that the linear operator $M$ defined on the base elements $z ^ { n }$ of $\Lambda$ by
\begin{equation} \tag{a2} M [ z ^ { n } ] = c _ { n } , n = 0 , \pm 1 , \pm 2 , \dots, \end{equation}
is positive on $( 0 , \infty )$, i.e. for any $L \in \Lambda$ such that $L ( z ) \geq 0$ for $z \in ( 0 , \infty )$ and $L ( z ) \not\equiv 0$, then $M [ L ] > 0$. An equivalent condition is that if
\begin{equation} \tag{a3} H _ { 0 } ^ { ( m ) } = 1 ,\, H _ { k } ^ { ( m ) } = \operatorname { det } ( c_{ m + i + j} ) _ { i ,\, j = 0 } ^ { k - 1 } \end{equation}
for $m = 0 , \pm 1 , \pm 2 , \dots$, $k = 1,2 , \dots$, are the Hankel determinants associated with $\{ c _ { k } \}$ (cf. also Hankel matrix), then
\begin{equation*} H _ { k } ^ { ( m ) } > 0 , m = 0 , \pm 1 , \pm 2 , \ldots , k = 1,2 ,\dots . \end{equation*}
Orthogonal Laurent polynomials $\{ Q _ { n } ( z ) \in \Lambda _ { n } : n = 0,1 , \ldots \}$ may be defined with respect to the inner product $\langle P , Q \rangle \equiv M [ P ( z ) Q ( z ) ]$ and are given by:
\begin{equation} \tag{a4} Q _ { 2 n } ( z ) = \frac { 1 } { H _ { 2 n } ^ { ( - 2 n ) } } \left| \begin{array} { c c c c } { c _ { - 2 n } } & { \cdots } & { c _ { - 1 } } & { z ^ { - n } } \\ { \vdots } & { \square } & { \vdots } & { \vdots } \\ { c _ { - 1 } } & { \cdots } & { c _ { 2 n - 2 } } & { z ^ { n - 1 } } \\ { c_0 } & { \cdots } & { c _ { 2 n - 1 } } & { z ^ { n } e n d } \end{array} \right|, \end{equation}
\begin{equation*} n = 1,2 , \dots , \end{equation*}
and
\begin{equation} \tag{a5} Q _ { 2 n + 1 } ( z ) = \frac { - 1 } { H _ { 2 n + 1 } ^ { ( - 2 n ) } } \left| \begin{array} { c c c c } { c_{ - 2 n - 1} } & { \cdots } & { c_{ - 1} } & { z ^ { - n - 1 } } \\ { \vdots } & { \square } & { \vdots } & { \vdots } \\ { c_{ - 1} } & { \cdots } & { c _ { 2 n - 1 } } & { z ^ { n - 1 } } \\ { c_0 } & { \cdots } & { c _ { 2 n } } & { z ^ { n } e n d } \end{array} \right|, \end{equation}
\begin{equation*} n = 0,1 , \ldots , \end{equation*}
and $Q _ { 0 } ( z ) = 1$. Corresponding associated orthogonal Laurent polynomials $\{ P _ { n } \}$ are defined by
\begin{equation} \tag{a6} P _ { n } = M \left[ \frac { Q _ { n } ( t ) - Q _ { n } ( z ) } { t - z } \right] , n = 0,1 ,\dots . \end{equation}
The rational functions $( - z ) P _ { n } ( - z ) / Q _ { n } ( - z )$ are the convergents of the positive T-fraction [a3],
\begin{equation} \tag{a7} \frac { F _ { 1 } z } { 1 + G _ { 1 } z } \square _ { + } \frac { F _ { 2 } z } { 1 + G _ { 2 } z } \square _ { + } \frac { F _ { 3 } } { 1 + G _ { 3 } z } \square _ { + } \dots \end{equation}
\begin{equation*} ( F _ { n } > 0 , G _ { n } > 0 ), \end{equation*}
where
\begin{equation*} F _ { n } = \frac { H _ { n } ^ { ( - n ) } H _ { n-2 } ^ { ( - n + 3 ) } } { H _ { n-1 } ^ { ( - n + 2 ) } H _ { n - 1 } ^ { ( - n + 1 ) } }, \end{equation*}
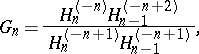 |
which corresponds to the formal pair of power series,
\begin{equation} \tag{a8} L _ { 0 } = - \sum _ { k = 1 } ^ { \infty } c _ { - k } ( - z ) ^ { k } , L _ { \infty } = \sum _ { k = 0 } ^ { \infty } c _ { k } ( - z ) ^ { - k }. \end{equation}
The T-fraction is equivalent to the continued fraction
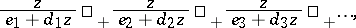 | (a9) |
where
\begin{equation} \tag{a10} F _ { n } = \frac { 1 } { e _ { n } e _ { n - 1} } ,\, G _ { n } = \frac { d _ { n } } { e _ { n } } ( e_{ 0} = 1 ), \end{equation}
\begin{equation*} n = 1,2 , \dots \end{equation*}
The following result may then be proved [a1]: The solution of the strong Stieltjes moment problem (a1) is unique if and only if at least one of the series $\sum e_{ n}$, $\sum d _ { n }$ diverges, and then
\begin{equation} \tag{a11} \operatorname { lim } _ { n \rightarrow \infty } \left[ ( - z ) \frac { P _ { n } ( - z ) } { Q _ { n } ( - z ) } \right] = z \int _ { 0 } ^ { \infty } \frac { d \psi ( t ) } { z + t }, \end{equation}
where $\psi ( t )$ is this unique solution.The convergence is uniform on every compact subset of $R = \{ z : | \operatorname { arg } z | < \pi \}$.
The strong Stieltjes moment problem is said to be determinate when it has a unique solution and indeterminate otherwise. A detailed discussion of the latter case has been given in [a4].
A classic example of a strong Stieltjes moment problem is the log-normal distribution,
\begin{equation*} \frac { d \psi ( t ) } { d t } = \frac { q ^ { 1 / 2 } } { 2 \kappa \sqrt { \pi } } e ^ { - ( \operatorname { ln } t / 2 \kappa ) ^ { 2 } } ,\, q = e ^ { - 2 \kappa ^ { 2 } }. \end{equation*}
(Cf. also Normal distribution.) The corresponding sequence of moments is $\{ c _ { n } \}$, where
\begin{equation*} c _ { n } = q ^ { - n - n ^ { 2 } / 2 } , n = 0 , \pm 1 , \pm 2 , \ldots , \end{equation*}
and the strong Stieltjes moment problem in this case is indeterminate [a5]. The moments corresponding to the log-normal distribution are related to a subclass of strong Stieltjes moment problems where
\begin{equation*} c _ { - n } = c _ { n } , \quad n = 1,2 , \dots . \end{equation*}
This subclass has been called strong symmetric Stieltjes moment problems by A.K. Common and J. McCabe, who studied properties of the related continued fractions [a6]. Other subclasses have been investigated in [a7].
Cf. also Moment problem.
References
| [a1] | W.B. Jones, O. Njåstad, W.J. Thron, "A strong Stieltjes moment problem" Trans. Amer. Math. Soc. , 261 (1980) pp. 503–528 |
| [a2] | W.B. Jones, O. Njåstad, W.J. Thron, "Continued fractions and strong Hamburger moment problems" Proc. London Math. Soc. , 47 (1983) pp. 105–123 |
| [a3] | W.B. Jones, W.J. Thron, "Continued fractions: Analytic theory and applications" , Encycl. Math. Appl. , 11 , Addison-Wesley (1980) |
| [a4] | O. Njåstad, "Solutions of the strong Stieltjes moment problem" Meth. Appl. Anal. , 2 (1995) pp. 320–347 |
| [a5] | S.C. Cooper, W.B. Jones, W.J. Thron, "Orthogonal Laurent polynomials and continued fractions associated with log-normal distributions" J. Comput. Appl. Math. , 32 (1990) pp. 39–46 |
| [a6] | A.K. Common, J. McCabe, "The symmetric strong moment problem" J. Comput. Appl. Math. , 67 (1996) pp. 327–341 |
| [a7] | A. Sri Ranga, E.X.L. de Andrade, J. McCabe, "Some consequences of symmetry in strong distributions" J. Math. Anal. Appl. , 193 (1995) pp. 158–168 |
Strong Stieltjes moment problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Strong_Stieltjes_moment_problem&oldid=14838