Straight line
One of the basic geometric concepts. A straight line is usually implicitly defined by the axioms of geometry; e.g., a Euclidean straight line by the axioms of incidence, order, congruence, and continuity. A straight line is called projective, affine, hyperbolic, etc., depending on the plane in which it is imbedded. A straight line can be studied by its transformations induced by the collineations of the plane. E.g., the group of algebraic automorphisms of a real projective straight line is isomorphic to the group of displacements of the Lobachevskii plane. Topologically, all straight lines in one plane are equivalent. Thus, the elliptic and real projective straight lines are topologically equivalent to a circle in the Euclidean plane, while the complex projective straight line is topologically equivalent to a two-dimensional sphere in the Euclidean space. A straight line is called continuous, discrete or finite if it is incident with a set of points of the cardinality of the continuum, with a countable set or with a finite set, respectively.
In the plane over an arbitrary algebraic field, a straight line is an algebraic curve of order one. In the rectilinear coordinate system  of the Euclidean plane
of the Euclidean plane  , a straight line is given by an equation
, a straight line is given by an equation
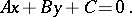 |
The coefficients  determine the coordinates of the normal vector of this straight line.
determine the coordinates of the normal vector of this straight line.
The straight line  in the affine space over a field
in the affine space over a field  (according to Weil) is the set of points
(according to Weil) is the set of points  for which
for which  , where
, where  .
.
Comments
Cf. also Hilbert system of axioms.
References
| [a1] | H.R. Jacobs, "Geometry" , Freeman (1974) |
Straight line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Straight_line&oldid=11779