Stone-Čech compactification
From Encyclopedia of Mathematics
Revision as of 07:55, 26 March 2012 by Ulf Rehmann (talk | contribs) (moved Stone-Cech compactification to Stone-Čech compactification: accented title)
The largest compactification 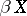 of a completely-regular space
of a completely-regular space 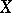 . Constructed by E. Čech [1] and M.H. Stone [2].
. Constructed by E. Čech [1] and M.H. Stone [2].
Let 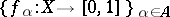 be the set of all continuous functions
be the set of all continuous functions 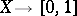 . The mapping
. The mapping 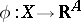 , where
, where 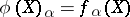 , is a homeomorphism onto its own image. Then, by definition,
, is a homeomorphism onto its own image. Then, by definition, 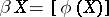 (where
(where  is the operation of closure). For any compactification
is the operation of closure). For any compactification 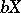 there exists a continuous mapping
there exists a continuous mapping 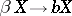 that is the identity on
that is the identity on 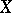 , a fact expressed by the word "largest" .
, a fact expressed by the word "largest" .
The Stone–Čech compactification of a quasi-normal space coincides with its Wallman compactification.
References
| [1] | E. Čech, "On bicompact spaces" Ann. of Math. , 38 (1937) pp. 823–844 |
| [2] | M.H. Stone, "Applications of the theory of Boolean rings to general topology" Trans. Amer. Soc. , 41 (1937) pp. 375–481 |
| [3] | R. Engelking, "Outline of general topology" , North-Holland (1968) (Translated from Polish) |
| [4] | P.S. Aleksandrov, "Some results in the theory of topological spaces, obtained within the last twenty-five years" Russian Math. Surveys , 15 : 2 (1960) pp. 23–83 Uspekhi Mat. Nauk , 15 : 2 (1960) pp. 25–95 |
Comments
Instead of Stone–Čech compactification one finds about equally frequently Čech–Stone compactification in the literature.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
| [a2] | L. Gillman, M. Jerison, "Rings of continuous functions" , Springer (1976) |
| [a3] | J.R. Porter, R.G. Woods, "Extensions and absolutes of Hausdorff spaces" , Springer (1988) |
| [a4] | R.C. Walker, "The Stone–Čech compactification" , Springer (1974) |
How to Cite This Entry:
Stone-Čech compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stone-%C4%8Cech_compactification&oldid=39436
Stone-Čech compactification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stone-%C4%8Cech_compactification&oldid=39436
This article was adapted from an original article by I.G. Koshevnikova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article