Stokes phenomenon

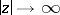The property that a function may have different asymptotic expressions when in different domains of the complex -plane. G. Stokes demonstrated [1] that the solution of the so-called Airy equation

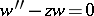which decreases for real 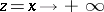, has the following asymptotic expansion when :

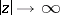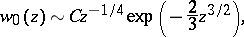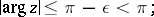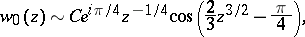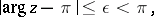where 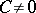is a constant. The function 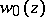is an entire function, while its asymptotic expansion is a discontinuous function.

The Stokes phenomenon also occurs for Laplace integrals, solutions of ordinary differential equations, etc. (see [2], [3]).

References

[1]	G.G. Stokes, Trans. Cambridge Philos. Soc. , 10 (1864) pp. 106–128
[2]	J. Heading, "An introduction to phase-integral methods" , Methuen (1962)
[3]	N.G. de Bruijn, "Asymptotic methods in analysis" , Dover, reprint (1981)

Comments

There is a recent interest in the Stokes phenomenon in asymptotic analysis, which is initiated by M.V. Berry in [a1]. In the new interpretation of the phenomenon, an error function is introduced to describe the rapid change in the behaviour of the remainders of the asymptotic expansions as a Stokes line is crossed. A rigorous treatment of Berry's observation is given in [a2].

References

[a1]	M.V. Berry, "Uniform asymptotic smoothing of Stokes' discontinuities" Proc. R. Soc. London A , 422 (1989) pp. 7–21
[a2]	"On Stokes's phenomenon and converging factors" R. Wong (ed.) , Proc. Int. Symp. Asymptotic and Computational Anal. (Winnipeg, Manitoba) , M. Dekker (1990)