Stochastic process with independent increments
A stochastic process 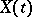 such that for any natural number
such that for any natural number  and all real
and all real 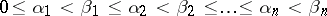 , the increments
, the increments
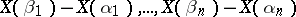 |
are mutually-independent random variables. A stochastic process with independent increments is called homogeneous if the probability distribution of 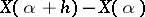 ,
, 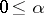 ,
, 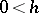 , depends only on
, depends only on 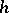 and not on
and not on  . Since the result of adding any non-random function
. Since the result of adding any non-random function 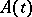 to
to 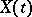 is again a stochastic process with independent increments, the realizations of such processes can be arbitrarily irregular. However, by suitably "centering" the process (say by subtracting from
is again a stochastic process with independent increments, the realizations of such processes can be arbitrarily irregular. However, by suitably "centering" the process (say by subtracting from 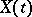 the function
the function 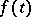 defined by the relation
defined by the relation 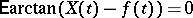 ), one can make more definite judgements about the structure of the "centred" process. There are at most countably-many (non-random) points
), one can make more definite judgements about the structure of the "centred" process. There are at most countably-many (non-random) points 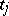 at which
at which 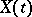 has random jumps
has random jumps
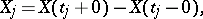 |
and the difference
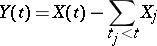 |
is a stochastically-continuous stochastic process with independent increments: for any 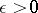 and
and 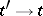 ,
,
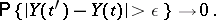 |
A Wiener process and a Poisson process are examples of stochastically-continuous stochastic processes with independent increments (and realizations of the first are continuous with probability one, while realizations of the second are step functions with jumps equal to one). An important example of a stochastic process with independent increments is that of a stable process (cf. Stable distribution). Realizations of a stochastically-continuous stochastic process with independent increments can only have discontinuities of the first kind, with probability one. The distribution of the values of such a process for any 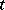 is infinitely divisible (see Infinitely-divisible distribution). In studying stochastic processes with independent increments one can apply the method of characteristic functions (cf. Characteristic function). Problems on the probability of a process crossing a boundary and on the probability distribution of the first crossing time are solved using the so-called factorization identities.
is infinitely divisible (see Infinitely-divisible distribution). In studying stochastic processes with independent increments one can apply the method of characteristic functions (cf. Characteristic function). Problems on the probability of a process crossing a boundary and on the probability distribution of the first crossing time are solved using the so-called factorization identities.
References
| [1] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) |
| [2] | A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) (Translated from Russian) |
Comments
For additional references see Stochastic process.
Stochastic process with independent increments. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_process_with_independent_increments&oldid=18314