Stochastic process, generalized
A stochastic process  depending on a continuous (time) argument
depending on a continuous (time) argument  and such that its values at fixed moments of time do not, in general, exist, but the process has only "smoothed values"
and such that its values at fixed moments of time do not, in general, exist, but the process has only "smoothed values"  describing the results of measuring its values by means of all possible linear measuring devices with sufficiently smooth weight function (or impulse transition function)
describing the results of measuring its values by means of all possible linear measuring devices with sufficiently smooth weight function (or impulse transition function)  . A generalized stochastic process
. A generalized stochastic process  is a continuous linear mapping of the space
is a continuous linear mapping of the space  of infinitely-differentiable functions
of infinitely-differentiable functions  of compact support (or any other space of test functions used in the theory of generalized functions) into the space
of compact support (or any other space of test functions used in the theory of generalized functions) into the space  of random variables
of random variables  defined on some probability space. Its realizations
defined on some probability space. Its realizations 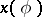 are ordinary generalized functions of the argument
are ordinary generalized functions of the argument  . Ordinary stochastic processes
. Ordinary stochastic processes 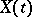 can also be regarded as generalized stochastic processes, for which
can also be regarded as generalized stochastic processes, for which
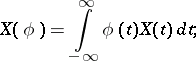 |
this is particularly useful in combination with the fact that a generalized stochastic process 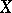 always has derivatives
always has derivatives 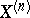 of any order
of any order  , given by
, given by
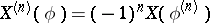 |
(see, for example, Stochastic process with stationary increments). The most important example of a generalized stochastic process of non-classical type is that of white noise. A generalization of the concept of a generalized stochastic process is that of a generalized random field.
For references, see Random field, generalized.
Comments
References
| [a1] | I.M. Gel'fand, N.Ya. Vilenkin, "Generalized functions. Applications of harmonic analysis" , 4 , Acad. Press (1964) (Translated from Russian) |
Stochastic process, generalized. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_process,_generalized&oldid=13436