Difference between revisions of "Stochastic matrix"
(→Comments: converted a reference range to an enumeration (a range make no sense with abbreviation-style references)) |
(TeXed the first few paragraphs) |
||
| Line 4: | Line 4: | ||
[[Category:Markov chains]] | [[Category:Markov chains]] | ||
| − | A square (possibly infinite) matrix | + | A stochastic matrix is a square (possibly infinite) matrix $P=[p_{ij}]$ with non-negative elements, for which |
| + | $$ | ||
| + | \sum_j p_{ij} = 1 \quad \text{for all $i$.} | ||
| + | $$ | ||
| + | The set of all stochastic matrices of order $n$ is the convex hull of the set of $n^n$ stochastic matrices consisting of zeros and ones. Any stochastic matrix $P$ can be considered as the [[Matrix of transition probabilities|matrix of transition probabilities]] of a discrete [[Markov chain|Markov chain]] $\xi^P(t)$. | ||
| − | + | The absolute values of the eigenvalues of stochastic matrices do not exceed 1; 1 is an eigenvalue of any stochastic matrix. If a stochastic matrix $P$ is indecomposable (the Markov chain $\xi^P(t)$ has one class of positive states), then 1 is a simple eigenvalue of $P$ (i.e. it has multiplicity 1); in general, the multiplicity of the eigenvalue 1 coincides with the number of classes of positive states of the Markov chain $\xi^P(t)$. If a stochastic matrix is indecomposable and if the class of positive states of the Markov chain has period $d$, then the set of all eigenvalues of $P$, as a set of points in the complex plane, is mapped onto itself by rotation through an angle $2\pi/d$. When $d=1$, the stochastic matrix $P$ and the Markov chain $\xi^P(t)$ are called aperiodic. | |
| − | + | The left eigenvectors $\pi = \{\pi_j\}$ of $P$ of finite order, corresponding to the eigenvalue 1: | |
| − | + | $$ | |
| − | + | \pi_j = \sum_i \pi_i p_{ij} \quad \text{for all $j$,} | |
| − | + | $$ | |
| − | The left eigenvectors | + | and satisfying the conditions $\pi_j \geq 0$, $\sum_j\pi_j = 1$, define the stationary distributions of the Markov chain $\xi^P(t)$; in the case of an indecomposable matrix $P$, the stationary distribution is unique. |
| − | |||
| − | |||
| − | |||
| − | and satisfying the conditions | ||
If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090150/s09015025.png" /> is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists: | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090150/s09015025.png" /> is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists: | ||
Revision as of 11:24, 30 May 2012
2020 Mathematics Subject Classification: Primary: 15B51 Secondary: 60J10 [MSN][ZBL]
A stochastic matrix is a square (possibly infinite) matrix $P=[p_{ij}]$ with non-negative elements, for which $$ \sum_j p_{ij} = 1 \quad \text{for all $i$.} $$ The set of all stochastic matrices of order $n$ is the convex hull of the set of $n^n$ stochastic matrices consisting of zeros and ones. Any stochastic matrix $P$ can be considered as the matrix of transition probabilities of a discrete Markov chain $\xi^P(t)$.
The absolute values of the eigenvalues of stochastic matrices do not exceed 1; 1 is an eigenvalue of any stochastic matrix. If a stochastic matrix $P$ is indecomposable (the Markov chain $\xi^P(t)$ has one class of positive states), then 1 is a simple eigenvalue of $P$ (i.e. it has multiplicity 1); in general, the multiplicity of the eigenvalue 1 coincides with the number of classes of positive states of the Markov chain $\xi^P(t)$. If a stochastic matrix is indecomposable and if the class of positive states of the Markov chain has period $d$, then the set of all eigenvalues of $P$, as a set of points in the complex plane, is mapped onto itself by rotation through an angle $2\pi/d$. When $d=1$, the stochastic matrix $P$ and the Markov chain $\xi^P(t)$ are called aperiodic.
The left eigenvectors $\pi = \{\pi_j\}$ of $P$ of finite order, corresponding to the eigenvalue 1: $$ \pi_j = \sum_i \pi_i p_{ij} \quad \text{for all $j$,} $$ and satisfying the conditions $\pi_j \geq 0$, $\sum_j\pi_j = 1$, define the stationary distributions of the Markov chain $\xi^P(t)$; in the case of an indecomposable matrix $P$, the stationary distribution is unique.
If 
is an indecomposable aperiodic stochastic matrix of finite order, then the following limit exists:
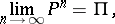 | (2) |
where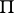 
is the matrix all rows of which coincide with the vector 
(see also Markov chain, ergodic; for infinite stochastic matrices 
, the system of equations (1) may have no non-zero non-negative solutions that satisfy the condition 
; in this case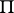 
is the zero matrix). The rate of convergence in (2) can be estimated by a geometric progression with any exponent 
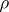that has absolute value greater than the absolute values of all the eigenvalues of 
other than 1.
If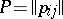 
is a stochastic matrix of order 
, then any of its eigenvalues 
satisfies the inequality (see [MM]):
 |
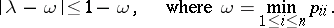The union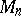 
of the sets of eigenvalues of all stochastic matrices of order 
has been described (see [Ka]).
A stochastic matrix 
that satisfies the extra condition
 |
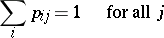is called a doubly-stochastic matrix. The set of doubly-stochastic matrices of order 
is the convex hull of the set of 
permutation matrices of order 
(i.e. doubly-stochastic matrices consisting of zeros and ones). A finite Markov chain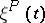 
with a doubly-stochastic matrix 
has the uniform stationary distribution.
References
| [G] | F.R. Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [B] | R. Bellman, "Introduction to matrix analysis" , McGraw-Hill (1960) MR0122820 Zbl 0124.01001 |
| [MM] | M. Marcus, H. Minc, "A survey of matrix theory and matrix inequalities" , Allyn & Bacon (1964) MR0162808 Zbl 0126.02404 |
| [Ka] | F.I. Karpelevich, "On the characteristic roots of matrices with non-negative entries" Izv. Akad. Nauk SSSR Ser. Mat. , 15 (1951) pp. 361–383 (In Russian) |
Comments
Given a real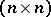 
-matrix 
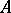with non-negative entries, the question arises whether there are invertible positive diagonal matrices 
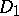and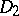 
such that 
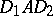is a doubly-stochastic matrix, and to what extent the 
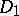and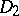 
are unique. Such theorems are known as 
-theorems. They are of interest in telecommunications and statistics, [C], [F], [Kr].
A matrix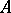 
is fully decomposable if there do not exist permutation matrices 
and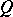 
such that
 |
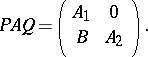A 
-matrix is fully indecomposable if it is non-zero.
Then for a non-negative square matrix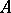 
there exist positive diagonal matrices 
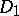and 
such that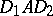 
is doubly stochastic if and only if there exist permutation matrices 
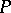and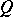 
such that 
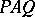is a direct sum of fully indecomposable matrices [SK], [BPS].
References
| [SK] | R. Sinkhorn, P. Knopp, "Concerning nonnegative matrices and doubly stochastic matrices" Pacific J. Math. , 21 (1967) pp. 343–348 MR0210731 Zbl 0152.01403 |
| [BPS] | R.A. Brualdi, S.V. Parter, H. Schneider, "The diagonal equivalence of a nonnegative matrix to a stochastic matrix" J. Math. Anal. Appl. , 16 (1966) pp. 31–50 MR0206019 Zbl 0231.15017 |
| [F] | S. Fienberg, "An iterative procedure for estimation in contingency tables" Ann. Math. Stat. , 41 (1970) pp. 907–917 MR0266394 Zbl 0198.23401 |
| [Kr] | R.S. Krupp, "Properties of Kruithof's projection method" Bell Systems Techn. J. , 58 (1979) pp. 517–538 |
| [C] | I. Csiszár, "I-divergence geometry of probability distributions and minimization problems" Ann. Probab. , 3 (1975) pp. 146–158 MR0365798 Zbl 0318.60013 |
| [Nu] | R.D. Nussbaum, "Iterated nonlinear maps and Hilbert's projective method II" Memoirs Amer. Math. Soc. , 401 (1989) |
| [Ne] | M.F. Neuts, "Structured stochastic matrices of 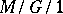 type and their applications" , M. Dekker (1989) MR1010040 Zbl 0695.60088
|
| [S] | E. Seneta, "Non-negative matrices and Markov chains" , Springer (1981) MR2209438 Zbl 0471.60001 |
Stochastic matrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_matrix&oldid=26956