Stochastic integral
An integral "∫ H dX" with respect to a semi-martingale  on some stochastic basis
on some stochastic basis  , defined for every locally bounded predictable process
, defined for every locally bounded predictable process 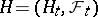 . One of the possible constructions of a stochastic integral is as follows. At first a stochastic integral is defined for simple predictable processes
. One of the possible constructions of a stochastic integral is as follows. At first a stochastic integral is defined for simple predictable processes 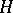 , of the form
, of the form
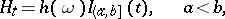 |
where 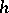 is
is  -measurable. In this case, by the stochastic integral
-measurable. In this case, by the stochastic integral 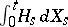 (or
(or  , or
, or  ) one understands the variable
) one understands the variable
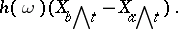 |
The mapping 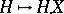 , where
, where
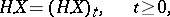 |
permits an extension (also denoted by  ) onto the set of all bounded predictable functions, which possesses the following properties:
) onto the set of all bounded predictable functions, which possesses the following properties:
a) the process 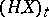 ,
, 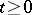 , is continuous from the right and has limits from the left;
, is continuous from the right and has limits from the left;
b)  is linear, i.e.
is linear, i.e.
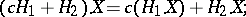 |
c) If 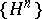 is a sequence of uniformly-bounded predictable functions,
is a sequence of uniformly-bounded predictable functions, 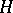 is a predictable function and
is a predictable function and
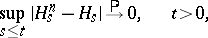 |
then
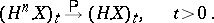 |
The extension 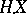 is therefore unique in the sense that if
is therefore unique in the sense that if 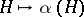 is another mapping with the properties a)–c), then
is another mapping with the properties a)–c), then 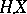 and
and 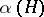 are stochastically indistinguishable (cf. Stochastic indistinguishability).
are stochastically indistinguishable (cf. Stochastic indistinguishability).
The definition
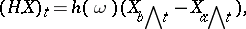 |
given for functions  holds for any process
holds for any process 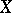 , not only for semi-martingales. The extension
, not only for semi-martingales. The extension 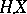 with properties a)–c) onto the class of bounded predictable processes is only possible for the case where
with properties a)–c) onto the class of bounded predictable processes is only possible for the case where 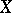 is a semi-martingale. In this sense, the class of semi-martingales is the maximal class for which a stochastic integral with the natural properties a)–c) is defined.
is a semi-martingale. In this sense, the class of semi-martingales is the maximal class for which a stochastic integral with the natural properties a)–c) is defined.
If 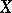 is a semi-martingale and
is a semi-martingale and 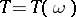 is a Markov time (stopping time), then the "stopped" process
is a Markov time (stopping time), then the "stopped" process 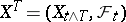 is also a semi-martingale and for every predictable bounded process
is also a semi-martingale and for every predictable bounded process 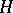 ,
,
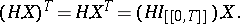 |
This property enables one to extend the definition of a stochastic integral to the case of locally-bounded predictable functions 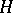 . If
. If 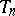 is a localizing (for
is a localizing (for 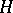 ) sequence of Markov times, then the
) sequence of Markov times, then the 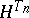 are bounded. Hence, the
are bounded. Hence, the 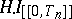 are bounded and
are bounded and
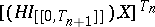 |
is stochastically indistinguishable from 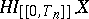 . A process
. A process  , again called a stochastic integral, therefore exists, such that
, again called a stochastic integral, therefore exists, such that
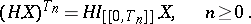 |
The constructed stochastic integral 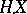 possesses the following properties:
possesses the following properties:  is a semi-martingale; the mapping
is a semi-martingale; the mapping 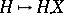 is linear; if
is linear; if  is a process of locally bounded variation, then so is the integral
is a process of locally bounded variation, then so is the integral 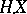 , and
, and 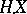 then coincides with the Stieltjes integral of
then coincides with the Stieltjes integral of 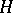 with respect to
with respect to  ;
; 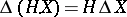 ;
;  .
.
Depending on extra assumptions concerning 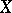 , the stochastic integral
, the stochastic integral 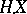 can also be defined for broader classes of functions
can also be defined for broader classes of functions 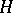 . For example, if
. For example, if 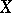 is a locally square-integrable martingale, then a stochastic integral
is a locally square-integrable martingale, then a stochastic integral 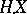 (with the properties a)–c)) can be defined for any predictable process
(with the properties a)–c)) can be defined for any predictable process 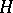 that possesses the property that the process
that possesses the property that the process
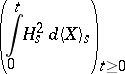 |
is locally integrable (here 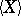 is the quadratic variation of
is the quadratic variation of 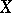 , i.e. the predictable increasing process such that
, i.e. the predictable increasing process such that  is a local martingale).
is a local martingale).
References
| [1] | J. Jacod, "Calcul stochastique et problèmes de martingales" , Lect. notes in math. , 714 , Springer (1979) |
| [2] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A-C , North-Holland (1978–1988) (Translated from French) |
| [3] | R.Sh. Liptser, A.N. [A.N. Shiryaev] Shiryayev, "Theory of martingales" , Kluwer (1989) (Translated from Russian) |
Comments
The result alluded to above, that semi-martingales constitute the widest viable class of stochastic integrators, is the Bichteler–Dellacherie theorem [a1]–[a3], and can be formulated as follows [a4], Thm. III.22. Call a process elementary predictable if it has a representation
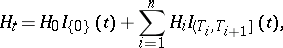 |
where 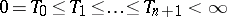 are stopping times and
are stopping times and 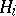 is
is 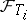 -measurable with
-measurable with 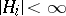 a.s.,
a.s., 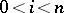 . Let
. Let 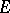 be the set of elementary predictable processes, topologized by uniform convergence in
be the set of elementary predictable processes, topologized by uniform convergence in 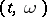 . Let
. Let 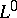 be the set of finite-valued random variables, topologized by convergence in probability. Fix a stochastic process
be the set of finite-valued random variables, topologized by convergence in probability. Fix a stochastic process 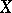 and for each stopping time
and for each stopping time 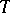 define a mapping
define a mapping 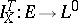 by
by
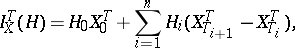 |
where 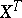 denotes the process
denotes the process 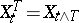 . Say that "X has the property (C)" if
. Say that "X has the property (C)" if 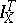 is continuous for all stopping times.
is continuous for all stopping times.
The Bichteler–Dellacherie theorem: 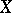 has property (C) if and only if
has property (C) if and only if 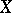 is a semi-martingale.
is a semi-martingale.
Since the topology on 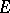 is very strong and that on
is very strong and that on 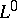 very weak, property (C) is a minimal requirement if the definition of
very weak, property (C) is a minimal requirement if the definition of 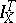 is to be extended beyond
is to be extended beyond 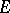 .
.
It is possible to use property (C) as the definition of a semi-martingale, and to develop the theory of stochastic integration from this point of view [a4]. There are many excellent textbook expositions of stochastic integration from the conventional point of view; see, e.g., [a5]–[a8].
References
| [a1] | K. Bichteler, "Stochastic integrators" Bull. Amer. Math. Soc. , 1 (1979) pp. 761–765 |
| [a2] | K. Bichteler, "Stochastic integrators and the  theory of semimartingales" Ann. Probab. , 9 (1981) pp. 49–89 theory of semimartingales" Ann. Probab. , 9 (1981) pp. 49–89 |
| [a3] | C. Dellacherie, "Un survol de la théorie de l'intégrale stochastique" Stoch. Proc. & Appl. , 10 (1980) pp. 115–144 |
| [a4] | P. Protter, "Stochastic integration and differential equations" , Springer (1990) |
| [a5] | K.L. Chung, R.J. Williams, "Introduction to stochastic integration" , Birkhäuser (1990) |
| [a6] | R.J. Elliott, "Stochastic calculus and applications" , Springer (1982) |
| [a7] | I. Karatzas, S.E. Shreve, "Brownian motion and stochastic calculus" , Springer (1988) |
| [a8] | L.C.G. Rogers, D. Williams, "Diffusions, Markov processes and martingales" , II. Ito calculus , Wiley (1987) |
| [a9] | H.P. McKean jr., "Stochastic integrals" , Acad. Press (1969) |
| [a10] | M. Metivier, J. Pellaumail, "Stochastic integration" , Acad. Press (1980) |
| [a11] | E.J. McShane, "Stochastic calculus and stochastic models" , Acad. Press (1974) |
| [a12] | M.M. Rao, "Stochastic processes and integration" , Sijthoff & Noordhoff (1979) |
| [a13] | D.W. Stroock, S.R.S. Varadhan, "Multidimensional diffusion processes" , Springer (1979) |
| [a14] | P.E. Kopp, "Martingales and stochastic integrals" , Cambridge Univ. Press (1984) |
| [a15] | M. Fukushima, "Dirichlet forms and Markov processes" , North-Holland (1980) |
| [a16] | S. Albeverio, J.E. Fenstad, R. Høegh-Krohn, T. Lindstrøm, "Nonstandard methods in stochastic analysis and mathematical physics" , Acad. Press (1986) |
Stochastic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_integral&oldid=15041