Stochastic indistinguishability
From Encyclopedia of Mathematics
A property of two random processes 
and 
which states that the random set
 |
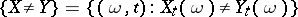can be disregarded, i.e. that the probability of the set 
is equal to zero. If 
and 
are stochastically indistinguishable, then 
for all 
, i.e. 
and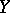 
are stochastically equivalent (cf. Stochastic equivalence). The opposite, generally speaking, is not true, but for processes that are continuous from the right (left), stochastic indistinguishability follows from stochastic equivalence.
References
| [1] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) |
Comments
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A , North-Holland (1978) (Translated from French) |
How to Cite This Entry:
Stochastic indistinguishability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_indistinguishability&oldid=13443
Stochastic indistinguishability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_indistinguishability&oldid=13443
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article