Stochastic geometry
A mathematical discipline in which one studies the relations between geometry and probability theory. Stochastic geometry developed from the classical integral geometry and from problems on geometric probabilities, with the introduction of ideas and methods from the theory of random processes, especially the theory of point processes.
One of the basic concepts of stochastic geometry is the concept of a process of geometric elements (a geometric process) in a "fundamental" space 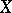 ; geometric processes are defined as point processes on manifolds that represent the space of (elementary) events. Thus, processes of straight lines in the plane are defined as point processes on the Möbius strip (the latter represents the space of straight lines in
; geometric processes are defined as point processes on manifolds that represent the space of (elementary) events. Thus, processes of straight lines in the plane are defined as point processes on the Möbius strip (the latter represents the space of straight lines in 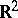 ). Other processes examined are processes of
). Other processes examined are processes of 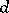 -dimensional planes in
-dimensional planes in 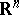 , processes of convex figures in
, processes of convex figures in 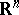 , of random mosaics in
, of random mosaics in 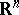 (the latter can be considered as processes of convex polyhedra such that the interiors of the polyhedra do not intersect with probability 1, while
(the latter can be considered as processes of convex polyhedra such that the interiors of the polyhedra do not intersect with probability 1, while 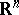 is equal to the union of their closures), etc.
is equal to the union of their closures), etc.
Processes on manifolds form a more general concept; here, stochastic geometry is linked with the theory of random sets (see [1]).
Another peculiarity, which distinguishes stochastic geometry from the theory of random sets, is the interest stochastic geometry has for geometric processes with distributions that are invariant relative to groups acting on the fundamental space 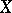 . The following is a characteristic result in this direction (see [2]). The class of those processes of straight lines on
. The following is a characteristic result in this direction (see [2]). The class of those processes of straight lines on 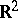 which possess finite intensity and which are invariant relative to the group of Euclidean motions of the plane is examined. A process is called non-singular if its Palm distribution is absolutely continuous relative to the (unconditional) distribution of the process. All non-singular processes of straight lines are doubly-stochastic Poisson processes (i.e. Poisson processes controlled by a random measure). For point processes in
which possess finite intensity and which are invariant relative to the group of Euclidean motions of the plane is examined. A process is called non-singular if its Palm distribution is absolutely continuous relative to the (unconditional) distribution of the process. All non-singular processes of straight lines are doubly-stochastic Poisson processes (i.e. Poisson processes controlled by a random measure). For point processes in 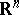 this does not hold.
this does not hold.
A number of no less unexpected properties of other geometric processes which are invariant relative to groups have been discovered using the tool of combinatorial integral geometry (see [3]). The following result, among others, has been obtained by the method of averaging combinatorial decompositions over the realization space of a process (see [3]). On  one examines a random set
one examines a random set  which is the union of domains from a certain process of convex domains which is invariant relative to the Euclidean group. Let
which is the union of domains from a certain process of convex domains which is invariant relative to the Euclidean group. Let 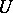 be a black set and let its complement be white. The alternating process of black and white intervals induced by the set
be a black set and let its complement be white. The alternating process of black and white intervals induced by the set 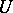 on the line
on the line 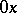 is said to be black-renewal if:
is said to be black-renewal if:
a) the white intervals  constitute an independent renewal process;
constitute an independent renewal process;
b) the triplets 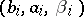 , where
, where 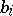 is the length of the
is the length of the 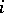 -th black interval and
-th black interval and 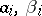 are the angles of intersection of
are the angles of intersection of 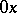 with
with 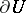 at the ends
at the ends  , for different
, for different 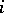 , are independent.
, are independent.
Under general assumptions of ergodicity and existence of certain moments, as well as when there are no rectilinear sections on 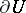 , it follows that if the process is black-renewal, the length of the white interval is distributed exponentially.
, it follows that if the process is black-renewal, the length of the white interval is distributed exponentially.
The concept of a "typical" element of a given geometric process is of considerable importance in stochastic geometry [7]. Problems of describing distributions that satisfy different conditions of "typical"  -subsets of elements in geometric processes have been studied (an example of such a problem is to find the distribution of Euclidean-invariant characteristics of a "typical" triangle with vertices as the realizations of a point process, whereby it is required that the interior of the triangle should contain
-subsets of elements in geometric processes have been studied (an example of such a problem is to find the distribution of Euclidean-invariant characteristics of a "typical" triangle with vertices as the realizations of a point process, whereby it is required that the interior of the triangle should contain 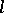 points from the realizations). The solution of such problems has been obtained for Poisson processes. Similar problems arise, for example, in astrophysics.
points from the realizations). The solution of such problems has been obtained for Poisson processes. Similar problems arise, for example, in astrophysics.
Problems of so-called stereology also relate to stochastic geometry if they are applied to processes of geometric figures [7]. (In stereology a multi-dimensional image has to be described through its intersections with straight lines or planes of a smaller number of dimensions.) Results have been obtained here on stereology of the first and second moment measures.
Only the most typical problems have been mentioned above, since the boundaries of stochastic geometry are hard to define accurately. The following areas adjoin stochastic geometry: geometric statistics [4], the theory of (random) sets of fractional dimensions [5], mathematical morphology and image analysis [6], random shape theory [7].
References
| [1] | J. Matheron, "Random sets and integral geometry" , Wiley (1975) |
| [2] | E.F. Harding, D.G. Kendall, "Stochastic geometry" , Wiley (1974) |
| [3] | R.V. [R.V. Ambartsumyan] Ambartzumian, "Combinatorial integral geometry" , Wiley (1982) |
| [4] | B.D. Ripley, "Spatial statistics" , Wiley (1981) |
| [5] | B.B. Mandelbrot, "Fractals: form, chance and dimension" , Freeman (1977) |
| [6] | J. Serra, "Image analysis and mathematical morphology" , Acad. Press (1988) |
| [7] | R.V. [R.V. Ambartsumyan] Ambartzumian, "Factorization calculus and geometric probability" , Cambridge Univ. Press (1989) (Translated from Russian) |
Comments
The more recent development of stochastic geometry, with a special view to various applications, is described in [a3]. The influence from integral geometry and its use in certain parts of stochastic geometry can be seen in [a4] and [a2]. A different point of view to some problems on geometric probabilities is the subject of [7].
References
| [a1] | R.V. Ambartzumian [R.V. Ambartsumyan] (ed.) , Stochastic and integral geometry , Reidel (1987) |
| [a2] | J. Mecke, R. Schneider, D. Stoyan, W. Weil, "Stochastische Geometrie" , DMV Sem. , 16 , Birkhäuser (1990) |
| [a3] | D. Stoyan, W.S. Kendall, J. Mecke, "Stochastic geometry and its applications" , Wiley (1987) |
| [a4] | L.A. Santaló, "Integral geometry and geometric probability" , Addison-Wesley (1976) |
Stochastic geometry. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_geometry&oldid=19188