Stochastic equivalence
The equivalence relation between random variables that differ only on a set of probability zero. More precisely, two random variables  and
and 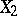 , defined on a common probability space
, defined on a common probability space  , are called stochastically equivalent if
, are called stochastically equivalent if  . In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
. In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
Two stochastic processes  and
and  ,
,  , defined on a common probability space are called stochastically equivalent if for any
, defined on a common probability space are called stochastically equivalent if for any  stochastic equivalence holds between the corresponding random variables:
stochastic equivalence holds between the corresponding random variables:  . With regard to stochastic processes
. With regard to stochastic processes 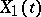 and
and 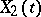 with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
Comments
The members of a stochastic equivalence class (of random variables or stochastic processes) are sometimes referred to as versions (of each other or of the equivalence class). A version of a random variable or stochastic process is also called a modification.
References
| [a1] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 |
| [a2] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1974) pp. 43ff (Translated from Russian) |
| [a3] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) pp. 46 |
| [a4] | A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 9 (Translated from Russian) |
| [a5] | R.Sh. Liptser, A.N. [A.N. Shiryaev] Shiryayev, "Theory of martingales" , Kluwer (1989) pp. 4 (Translated from Russian) |
Stochastic equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_equivalence&oldid=17201