Difference between revisions of "Stochastic equivalence"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
The equivalence relation between random variables that differ only on a set of probability zero. More precisely, two random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900901.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900902.png" />, defined on a common probability space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900903.png" />, are called stochastically equivalent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900904.png" />. In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves. | The equivalence relation between random variables that differ only on a set of probability zero. More precisely, two random variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900901.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900902.png" />, defined on a common probability space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900903.png" />, are called stochastically equivalent if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900904.png" />. In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves. | ||
| − | Two stochastic processes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900905.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900906.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900907.png" />, defined on a common probability space are called stochastically equivalent if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900908.png" /> stochastic equivalence holds between the corresponding random variables: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900909.png" />. With regard to stochastic processes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s09009010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s09009011.png" /> with coinciding finite-dimensional distributions, the term | + | Two stochastic processes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900905.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900906.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900907.png" />, defined on a common probability space are called stochastically equivalent if for any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900908.png" /> stochastic equivalence holds between the corresponding random variables: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s0900909.png" />. With regard to stochastic processes <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s09009010.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090090/s09009011.png" /> with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense. |
| Line 9: | Line 9: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 {{MR|0731258}} {{ZBL|0549.31001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , '''1''' , Springer (1974) pp. 43ff (Translated from Russian) {{MR|0346882}} {{ZBL|0291.60019}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) pp. 46 {{MR|0448504}} {{ZBL|0246.60032}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 9 (Translated from Russian) {{MR|1155400}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> R.Sh. Liptser, A.N. [A.N. Shiryaev] Shiryayev, "Theory of martingales" , Kluwer (1989) pp. 4 (Translated from Russian) {{MR|1022664}} {{ZBL|0728.60048}} </TD></TR></table> |
Revision as of 10:32, 27 March 2012
The equivalence relation between random variables that differ only on a set of probability zero. More precisely, two random variables  and
and 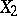 , defined on a common probability space
, defined on a common probability space  , are called stochastically equivalent if
, are called stochastically equivalent if  . In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
. In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
Two stochastic processes  and
and  ,
,  , defined on a common probability space are called stochastically equivalent if for any
, defined on a common probability space are called stochastically equivalent if for any  stochastic equivalence holds between the corresponding random variables:
stochastic equivalence holds between the corresponding random variables:  . With regard to stochastic processes
. With regard to stochastic processes 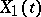 and
and 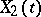 with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
Comments
The members of a stochastic equivalence class (of random variables or stochastic processes) are sometimes referred to as versions (of each other or of the equivalence class). A version of a random variable or stochastic process is also called a modification.
References
| [a1] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 MR0731258 Zbl 0549.31001 |
| [a2] | I.I. [I.I. Gikhman] Gihman, A.V. [A.V. Skorokhod] Skorohod, "The theory of stochastic processes" , 1 , Springer (1974) pp. 43ff (Translated from Russian) MR0346882 Zbl 0291.60019 |
| [a3] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) pp. 46 MR0448504 Zbl 0246.60032 |
| [a4] | A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 9 (Translated from Russian) MR1155400 |
| [a5] | R.Sh. Liptser, A.N. [A.N. Shiryaev] Shiryayev, "Theory of martingales" , Kluwer (1989) pp. 4 (Translated from Russian) MR1022664 Zbl 0728.60048 |
Stochastic equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_equivalence&oldid=17201