A system of ordinary differential equations in the numerical solution of which by explicit methods of Runge–Kutta or Adams type, the integration step has to remain small despite the slow change in the desired variables. Attempts to reduce the time for calculating the solution of a stiff differential system at the expense of increasing the integration step lead to a sharp increase in the error (error explosion).
An autonomous system of ordinary differential equations
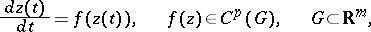 | (1) |
is said to be stiff if, for any initial values 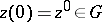 , the following conditions are satisfied on a given interval
, the following conditions are satisfied on a given interval 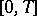 contained in the interval of existence of a solution of (1):
contained in the interval of existence of a solution of (1):
a) the maximum modulus of the eigenvalues of the Jacobi matrix (the spectral radius) is bounded along the solution 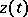 :
:
b) there exist numbers 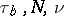 such that if
such that if
then the inequality
is satisfied; here
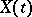 is the fundamental matrix of the system (1),
is the fundamental matrix of the system (1),
and 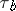 is the length of the boundary layer. All systems of type (1) for which the conditions a) and b) are satisfied simultaneously after scaling the components of the vectors
is the length of the boundary layer. All systems of type (1) for which the conditions a) and b) are satisfied simultaneously after scaling the components of the vectors 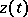 for each solution, are called stiff.
for each solution, are called stiff.
A non-autonomous normal system of ordinary differential equations of order 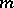 is said to be stiff if the autonomous system of order
is said to be stiff if the autonomous system of order 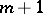 equivalent to it is stiff. The following scalar equation is an example of a stiff non-autonomous equation:
equivalent to it is stiff. The following scalar equation is an example of a stiff non-autonomous equation:
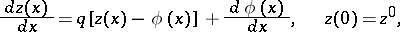 | (2) |
where 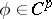 ,
, 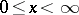 , is a given function. Another example of a stiff differential system is the linear homogeneous system
, is a given function. Another example of a stiff differential system is the linear homogeneous system
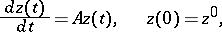 | (3) |
with constant 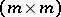 -matrix
-matrix 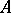 having different eigenvalues divided into two groups:
having different eigenvalues divided into two groups:
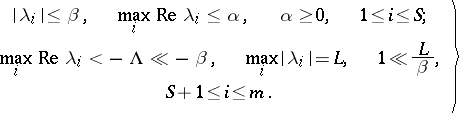 | (4) |
Condition a) is obviously satisfied for (3). The norm is bounded above by 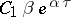 for
for  , where
, where 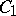 and
and 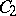 are certain constants. When
are certain constants. When 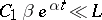 ,
, 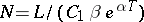 , condition b) is satisfied. The vector
, condition b) is satisfied. The vector 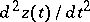 is bounded above if
is bounded above if 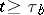 :
:
Thus it is possible to construct for 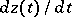 an algebraic interpolation polynomial of degree zero when
an algebraic interpolation polynomial of degree zero when 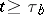 , with uniformly-distributed nodes, and to express the interpolation step in the form
, with uniformly-distributed nodes, and to express the interpolation step in the form 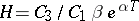 , where
, where 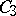 is some constant (see [1]) depending on the given error. On the other hand, use of Euler's polygonal method for (3) requires an upper bound on the size of the integration step on the entire interval of a solution of the system (see [1]):
is some constant (see [1]) depending on the given error. On the other hand, use of Euler's polygonal method for (3) requires an upper bound on the size of the integration step on the entire interval of a solution of the system (see [1]):
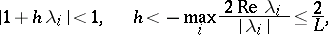 | (5) |
Here the components of the approximate solution to the system (3) by Euler's polygonal method corresponding to the first group of eigenvalues (4) will be represented with sufficient accuracy (see [1]):
Restrictions of the form (5) on the integration step are characteristic for extrapolation methods of Runge–Kutta or Adams type. The quotient 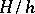 , which can be regarded as a qualitative measure of the stiffness of the system (3), attains values of order
, which can be regarded as a qualitative measure of the stiffness of the system (3), attains values of order 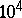 –
–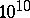 in many cases. The mathematical descriptions of dynamical processes and phenomena in physics, chemistry, biology, technology, and economics connected with the calculation of an ever larger number of factors raising the order of the differential systems, lead to an increase in stiffness. Stiff differential systems require special methods of solution.
in many cases. The mathematical descriptions of dynamical processes and phenomena in physics, chemistry, biology, technology, and economics connected with the calculation of an ever larger number of factors raising the order of the differential systems, lead to an increase in stiffness. Stiff differential systems require special methods of solution.
In certain cases, the original system (1) can be transformed using the theory of, and asymptotic methods for, differential equations with a small parameter in front of the leading derivatives, the behaviour of the solution of which in the boundary layer is described in terms of exponentially-damped functions (see [2]). However, it is usually difficult to reduce a stiff differential system to a similar form, and, moreover, the stiffness is not always essentially decreased after asymptotic transformation. Thus, numerical methods are used to solve systems of a general form. The main property of these methods is that they guarantee a suppression of the rapidly-damping components of the solution of (1) outside the boundary layer for a value of the integration step used near to that of the algebraic interpolation step.
It is appropriate to use implicit methods (see [9], [17]) in the solution of stiff differential systems. To construct implicit schemes, the method of undetermined coefficients can be used. On the basis of Taylor's formula it can be written in the form
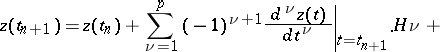 | (6) |
where  is a positive integer,
is a positive integer, 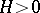 ,
, 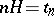 . For example, such methods are described in [9]:
. For example, such methods are described in [9]:
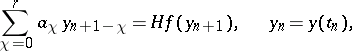 | (7) |
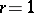 ,
, 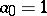 ,
, 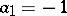 — the implicit polygonal method;
— the implicit polygonal method;
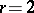 ,
, 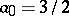 ,
, 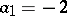 ,
, 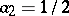 — the implicit
— the implicit  -nd order method;
-nd order method;
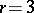 ,
, 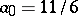 ,
, 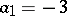 ,
, 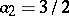 ,
, 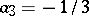 — the implicit
— the implicit  -rd order method;
-rd order method;
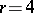 ,
, 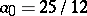 ,
, 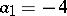 ,
, 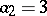 ,
, 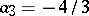 ,
, 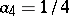 — the implicit 4th order method.
— the implicit 4th order method.
By the order of a method is understood the highest power 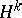 in the expansion (7) in powers of
in the expansion (7) in powers of 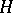 whose coefficient is the same as the corresponding coefficient in (6).
whose coefficient is the same as the corresponding coefficient in (6).
Application of the implicit polygonal method to the system (3) leads to the difference equations
 | (8) |
Suppose that the system (3) is asymptotically Lyapunov stable. Then the matrix 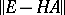 is non-singular for all
is non-singular for all  . The Lagrange–Sylvester formula can be used to represent the solution of (8) in the form
. The Lagrange–Sylvester formula can be used to represent the solution of (8) in the form
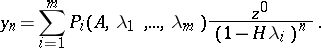 | (9) |
For the implicit polygonal method (8), the condition of asymptotic stability,
is satisfied for all  , and in (9) the components of the solution corresponding to the second group of eigenvalues (4) will be rapidly decreasing with increasing
, and in (9) the components of the solution corresponding to the second group of eigenvalues (4) will be rapidly decreasing with increasing  . The value of
. The value of  is restricted only by the requirements of the desired accuracy of the approximate solutions. The tendency to raise the order of linear multi-step methods leads to a definite contradiction to their stability (see [11]).
is restricted only by the requirements of the desired accuracy of the approximate solutions. The tendency to raise the order of linear multi-step methods leads to a definite contradiction to their stability (see [11]).
The  -step method
-step method
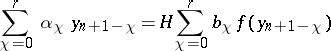 | (10) |
is said to be 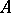 -stable if all solutions of (10) tend to zero as
-stable if all solutions of (10) tend to zero as 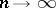 for a fixed positive
for a fixed positive 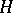 in the case when (10) is applied to the scalar equation
in the case when (10) is applied to the scalar equation
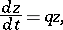 | (11) |
with 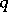 a complex constant with negative real part. An explicit
a complex constant with negative real part. An explicit  -step method cannot be
-step method cannot be 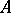 -stable. The order of a linear multi-step
-stable. The order of a linear multi-step 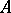 -stable method cannot exceed two. The smallest error constant
-stable method cannot exceed two. The smallest error constant 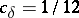 is obtained for the implicit trapezium method (see [11]):
is obtained for the implicit trapezium method (see [11]):
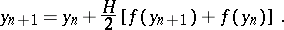 | (12) |
The requirement of  -stability imposes less rigid restrictions on the methods, unlike
-stability imposes less rigid restrictions on the methods, unlike 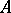 -stability. The
-stability. The  -step method (10) for fixed
-step method (10) for fixed 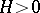 is said to be
is said to be 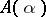 -stable if all solutions of (10) tend to zero as
-stable if all solutions of (10) tend to zero as 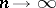 when (10) is applied to the equation (11), with
when (10) is applied to the equation (11), with 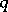 a complex constant in the set
a complex constant in the set
where 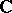 is the complex plane. An explicit
is the complex plane. An explicit  -step method cannot be
-step method cannot be 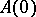 -stable. There exists only one
-stable. There exists only one 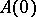 -stable
-stable  -step method of order
-step method of order 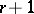 , namely (12). For
, namely (12). For 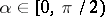 , there exist
, there exist 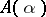 -stable methods of order
-stable methods of order  with
with 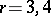 (see [13]).
(see [13]).
The following weakening of the requirement of 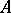 -stability is contained in the so-called definition of Gear (see [14]): (10) is said to be a stiffly-stable method if all solutions of (10) tend to zero as
-stability is contained in the so-called definition of Gear (see [14]): (10) is said to be a stiffly-stable method if all solutions of (10) tend to zero as 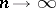 when (10) is applied to equation (11).
when (10) is applied to equation (11). 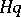 is a complex constant in
is a complex constant in 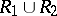 , where
, where
and the given accuracy is guaranteed for 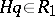 .
.
Method (7) is stiffly stable, and thus 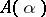 -stable. In these methods,
-stable. In these methods, 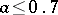 .
.
In accordance with (16), implicit analogues of the explicit Runge–Kutta methods of arbitrary order can be constructed that are moreover 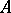 -stable and stiffly stable. For example, the
-stable and stiffly stable. For example, the  -nd order method
-nd order method
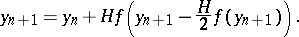 | (13) |
Application of (13) to (3) leads to the difference equations
which prove that it is 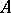 -stable. Similarly, for the
-stable. Similarly, for the  -rd order method
-rd order method
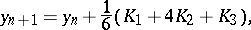 | (14) |
the following difference equations are similarly obtained:
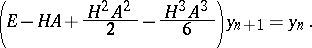 |
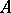 -stable and stiffly-stable methods of higher order are constructed in the same way. Methods (13) and (14), and those published in [5], are fundamentally different from the so-called implicit Runge–Kutta methods (see [16]), which have not become widely known because of their greater computational laboriousness. Application of implicit methods requires more computational effort at each step than is the case for explicit methods, but this is justified in stiff differential systems at the expense of a sharp increase in the size of the integration step. To solve (3), it is necessary to invert a matrix or to solve a system of linear equations. Here the problem of ill conditioning may arise, because the number of conditions on the matrix
-stable and stiffly-stable methods of higher order are constructed in the same way. Methods (13) and (14), and those published in [5], are fundamentally different from the so-called implicit Runge–Kutta methods (see [16]), which have not become widely known because of their greater computational laboriousness. Application of implicit methods requires more computational effort at each step than is the case for explicit methods, but this is justified in stiff differential systems at the expense of a sharp increase in the size of the integration step. To solve (3), it is necessary to invert a matrix or to solve a system of linear equations. Here the problem of ill conditioning may arise, because the number of conditions on the matrix 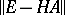 increases as
increases as 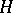 increases. In the general case of (1), at every integration step it is necessary to solve a non-linear system of equations for the vector
increases. In the general case of (1), at every integration step it is necessary to solve a non-linear system of equations for the vector 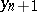 . It is common to use a modification of Newton's method with the initial condition calculated from an arbitrary extrapolation formula, using
. It is common to use a modification of Newton's method with the initial condition calculated from an arbitrary extrapolation formula, using 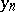 . The extrapolation method is then said to be a predictor and the implicit method a corrector. The method of simple iteration is inapplicable in stiff differential systems because of the large values of
. The extrapolation method is then said to be a predictor and the implicit method a corrector. The method of simple iteration is inapplicable in stiff differential systems because of the large values of 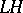 . Since Newton's method is applied in implicit schemes to solve the equations
. Since Newton's method is applied in implicit schemes to solve the equations 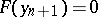 , and thus it is necessary to compute the Jacobi matrix of (1), this matrix is sometimes inserted directly into the formulas of the methods that also have the property of
, and thus it is necessary to compute the Jacobi matrix of (1), this matrix is sometimes inserted directly into the formulas of the methods that also have the property of 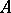 -stability for the solution of linear systems (see [12], [15]). Gear's procedure (Gear's method) is widely applied in the solution of stiff differential systems with automatic control of the error at each step, whence it alters the order of the method or the step size. Methods (7) are also used as correctors in Gear's procedure (see [9]). Another approach to the creation of methods for the integration of stiff systems of equations is connected with a calculation of the corresponding linear systems in the formulas of the solution methods (see [4]–[8], [10]). In the first articles in this direction, stiff systems of equations were discussed that had known eigenvalues for the matrix
-stability for the solution of linear systems (see [12], [15]). Gear's procedure (Gear's method) is widely applied in the solution of stiff differential systems with automatic control of the error at each step, whence it alters the order of the method or the step size. Methods (7) are also used as correctors in Gear's procedure (see [9]). Another approach to the creation of methods for the integration of stiff systems of equations is connected with a calculation of the corresponding linear systems in the formulas of the solution methods (see [4]–[8], [10]). In the first articles in this direction, stiff systems of equations were discussed that had known eigenvalues for the matrix 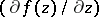 , according to which the matrix entries of the methods were constructed. Because of the difficulty of solving the eigenvalue problem, this direction was not developed for a considerable time. In [6], [7], [8], methods for constructing the matrix entries were proposed that did not require the solution of the eigenvalue problem for the matrix
, according to which the matrix entries of the methods were constructed. Because of the difficulty of solving the eigenvalue problem, this direction was not developed for a considerable time. In [6], [7], [8], methods for constructing the matrix entries were proposed that did not require the solution of the eigenvalue problem for the matrix 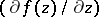 of the system (1). The methods in this direction can be constructed on the basis of the following equation (see [7]):
of the system (1). The methods in this direction can be constructed on the basis of the following equation (see [7]):
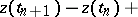 | (15) |
where 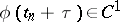 ,
, 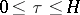 , is a non-singular (
, is a non-singular (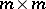 )-matrix and
)-matrix and 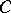 is a matrix not depending on
is a matrix not depending on  .
.
A different choice of the matrices 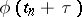 and
and 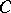 leads to difference equations corresponding to some method of numerical integration if the right-hand side of (15) is disregarded. For
leads to difference equations corresponding to some method of numerical integration if the right-hand side of (15) is disregarded. For 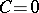 , explicit methods are obtained, and for
, explicit methods are obtained, and for 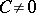 — implicit methods. Suppose that
— implicit methods. Suppose that 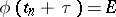 . Then the implicit polygonal method (7) corresponds to
. Then the implicit polygonal method (7) corresponds to 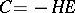 ; the trapezium method (12) to
; the trapezium method (12) to 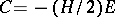 ; and the explicit polygonal method to
; and the explicit polygonal method to 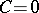 . When
. When 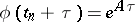 , where
, where 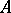 is a constant (
is a constant (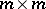 )-matrix, a generalized polygonal method is obtained (see [7]):
)-matrix, a generalized polygonal method is obtained (see [7]):
 | (16) |
Formula (16) becomes the explicit polygonal method when  . Method (16) gives an exact solution of the system of equations
. Method (16) gives an exact solution of the system of equations
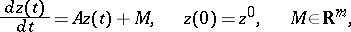 | (17) |
for the discrete values 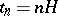 . If the matrix
. If the matrix
is known, then 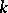 iterations of the recurrence relation
iterations of the recurrence relation
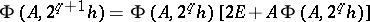 | (18) |
leads to the matrix
applied in (16). As a first approximation to (18) for sufficiently-small 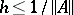 , it is appropriate to use the approximation formula
, it is appropriate to use the approximation formula
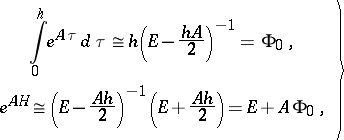 | (19) |
or, if the eigenvalues of the matrix are real,
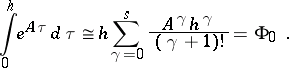 | (20) |
Formula (19) gives a Lyapunov-stable correspondence between solutions of the differential system (17) and of the difference system (16) when 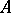 has complex eigenvalues with small real part. If the domain
has complex eigenvalues with small real part. If the domain 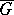 of existence of the solutions is closed, convex in
of existence of the solutions is closed, convex in  , and if the approximate solutions belong to this domain, then the error in (16) satisfies the following difference equation (see [7]):
, and if the approximate solutions belong to this domain, then the error in (16) satisfies the following difference equation (see [7]):
where 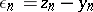 and
and  ,
, 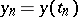 are solutions of (1) and (16), respectively. Let
are solutions of (1) and (16), respectively. Let  be the norm of the vector (the norms of the matrices are subordinated to this vector norm), and suppose that the following inequalities are satisfied in
be the norm of the vector (the norms of the matrices are subordinated to this vector norm), and suppose that the following inequalities are satisfied in 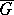 :
:
The following number is computed for a real matrix 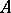 :
:
Then the following estimates hold:
If 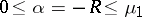 , the error
, the error 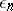 can be estimated on the assumption that
can be estimated on the assumption that 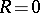 . Other vector norms are possible in the estimates, with corresponding matrix norms and logarithmic norms (see [3]). These estimates prove that in the solution of (1), the integration step
. Other vector norms are possible in the estimates, with corresponding matrix norms and logarithmic norms (see [3]). These estimates prove that in the solution of (1), the integration step 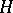 can be taken significantly larger than in classical methods. The matrix
can be taken significantly larger than in classical methods. The matrix 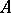 must be chosen in such a way that all its entries are close to those of the Jacobi matrix of the system (1). In the boundary layer, when the variables change rapidly, by estimating
must be chosen in such a way that all its entries are close to those of the Jacobi matrix of the system (1). In the boundary layer, when the variables change rapidly, by estimating 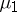 ,
, 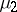 ,
, 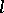 , and
, and 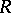 roughly for the approximate solution, it is possible to change
roughly for the approximate solution, it is possible to change 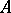 so as to obtain the necessary accuracy. Since the variables in (1) change slowly across the boundary layer, it often turns out that one matrix
so as to obtain the necessary accuracy. Since the variables in (1) change slowly across the boundary layer, it often turns out that one matrix 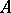 is sufficient to compute all solutions when
is sufficient to compute all solutions when 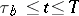 . The checking of the accuracy can be accomplished by using Runge's rule (see [1]).
. The checking of the accuracy can be accomplished by using Runge's rule (see [1]).
To increase the accuracy, a class of methods for the numerical integration of systems has been suggested in [7], based on the method (16). The following requirements are satisfied for the methods in this class: 1) an  -th order method must be exact for the integration of algebraic polynomials of degree
-th order method must be exact for the integration of algebraic polynomials of degree 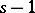 when
when 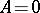 ; and 2) a method of arbitrary order must be exact for the solution of (17).
; and 2) a method of arbitrary order must be exact for the solution of (17).
The one-step  -nd order method has the form:
-nd order method has the form:
Explicit one-step 3th order methods and multi-step methods for systems are constructed in the same way. Asymptotic estimates for the errors have been found. For 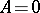 , these methods become formulas of Runge–Kutta or Adams type. In the approximation to integrals of
, these methods become formulas of Runge–Kutta or Adams type. In the approximation to integrals of 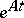 by fractional-linear matrix polynomials in
by fractional-linear matrix polynomials in 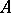 , taking into account the non-singularity of the corresponding matrices, the methods for systems go over to the explicit formulas of the corresponding implicit methods obtained after iteration by Newton's method. The following is an implicit
, taking into account the non-singularity of the corresponding matrices, the methods for systems go over to the explicit formulas of the corresponding implicit methods obtained after iteration by Newton's method. The following is an implicit 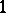 -st order method for systems:
-st order method for systems:
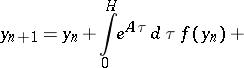 | (21) |
It is obtained from (15) if one chooses
The equations (21) are obtained by the method of reducing differential equations to integral equations (see [8]). The integral of 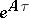 in (21) is calculated according to (18) with the initial condition (20). A method of correction of this integral in the course of solving has been investigated (see ).
in (21) is calculated according to (18) with the initial condition (20). A method of correction of this integral in the course of solving has been investigated (see ).
References
| [1] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [2] | A.B. Vasil'eva, "Constructions of uniform approximations to solutions of systems of differential equations with small parameter in front of the leading derivative" Mat. Sb. , 50 (1960) pp. 43–58 (In Russian) |
| [3] | B.F. Bylov, R.E. Vinograd, D.M. Grobman, V.V. Nemytskii, "The theory of Lyapunov exponents and its applications to problems of stability" , Moscow (1966) (In Russian) |
| [4] | M.K. Gavurin, "An experiment in the numerical integration of ordinary differential equations" Met. Vychisl. , 1 (1963) pp. 45–51 (In Russian) |
| [5] | Yu.V. Rakitskii, "Asymptotic error formulas for solutions of systems of ordinary differential equations by functional numerical methods" Soviet Math. Dokl. , 11 : 4 (1970) pp. 861–863 Dokl. Akad. Nauk SSSR , 193 : 1 (1970) pp. 40–42 |
| [6] | Yu.V. Rakitskii, "Methods for successive step increase in the numerical integration of systems of ordinary differential equations" Soviet Math. Dokl. , 13 : 6 (1972) pp. 1624–1627 Dokl. Akad. Nauk SSSR , 207 : 4 (1972) pp. 793–795 |
| [7] | Yu.V. Rakitskii, Trudy Leningrad. Polytech. Inst. , 332 (1973) pp. 88–97 |
| [8] | B.V. Pavlov, A.Ya. Povzner, "A method for the numerical integration of systems of ordinary differential equations" USSR Comp. Math. Math. Phys. , 13 : 4 (1973) pp. 292–297 Zh. Vychisl. Mat. i Mat. Fiz. , 13 : 4 (1973) pp. 1056–1059 |
| [9] | C.F. Curtiss, J.O. Hirschfelder, Proc. Nat. Acad. Sci. USA , 38 (1962) pp. 235–243 |
| [10] | R.H.S. Mah, S. Michaelson, R.W. Sargent, J. Chem. Eng. Sci. , 17 (1962) pp. 619–639 |
| [11] | G. Dahlquist, "A special stability problem for linear multistep methods" Nordisk. Tidskr. Informationsbehandling , 3 (1963) pp. 27–43 |
| [12] | H.H. Rosenbrock, "Some general implicit processes for the numerical solution of differential equations" Comput. J. , 5 (1963) pp. 329–330 |
| [13] | O.B. Widlund, "A note on unconditionally stable linear multistep methods" Nordisk. Tidskr. Informationsbehandling , 7 (1967) pp. 65–70 |
| [14] | C.W. Gear, "The automatic integration of stiff ordinary differential equations (with discussion)" , Information processing 68 , 1 , North-Holland (1969) pp. 187–193 |
| [15] | J.D. Lambert, S.T. Sigurdsson, "Multistep methods with variable matrix coefficients" SIAM J. Numer. Anal. , 9 (1972) pp. 715–733 |
| [16] | J.D. Lambert, "Computational methods in ordinary differential equations" , Wiley (1973) |
| [17] | R.A. Willoughby (ed.) , Stiff differential systems , The IBM research symposia series , Plenum (1974) |
The use of asymptotic methods for the system (1) as described in [2] has also been investigated in [a1]. The development of numerical methods for stiff differential equations was stimulated by [a2]. A number of theses has recently been devoted to this subject. For an introduction to the theory of stiff differential equations, [a3] can be used as reference.
References
| [a1] | J.E. Flaherty, R.E. O'Malley, "Numerical methods for stiff systems of two-point boundary value problems" SIAM J. Sci. and Statist. Comp. , 5 (1984) pp. 865–886 |
| [a2] | W. Lininger, R.A. Willoughby, "Efficient integration methods for stiff systems of ordinary differential equations" SIAM J. Numer. Anal. , 7 (1970) pp. 47–66 |
| [a3] | K. Dekker, J.G. Verwer, "Stability of Runge–Kutta methods for stiff nonlinear differential equations" , CWI Monographs , 2 , North-Holland (1984) |
| [a4] | W.L. Mirankar, "Numerical methods for stiff equations" , Reidel (1981) |
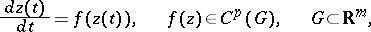
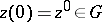 , the following conditions are satisfied on a given interval
, the following conditions are satisfied on a given interval 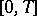 contained in the interval of existence of a solution of (1):
contained in the interval of existence of a solution of (1):
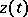 :
:
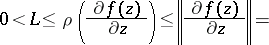
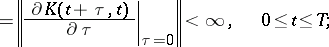
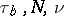 such that if
such that if
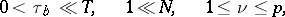
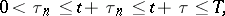
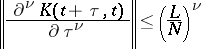
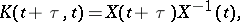
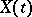 is the fundamental matrix of the system (1),
is the fundamental matrix of the system (1),
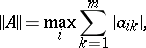
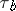 is the length of the boundary layer. All systems of type (1) for which the conditions a) and b) are satisfied simultaneously after scaling the components of the vectors
is the length of the boundary layer. All systems of type (1) for which the conditions a) and b) are satisfied simultaneously after scaling the components of the vectors 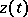 for each solution, are called stiff.
for each solution, are called stiff.
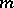 is said to be stiff if the autonomous system of order
is said to be stiff if the autonomous system of order 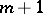 equivalent to it is stiff. The following scalar equation is an example of a stiff non-autonomous equation:
equivalent to it is stiff. The following scalar equation is an example of a stiff non-autonomous equation:
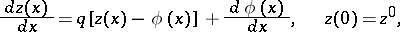
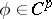 ,
, 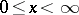 , is a given function. Another example of a stiff differential system is the linear homogeneous system
, is a given function. Another example of a stiff differential system is the linear homogeneous system
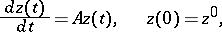
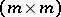 -matrix
-matrix 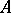 having different eigenvalues divided into two groups:
having different eigenvalues divided into two groups:
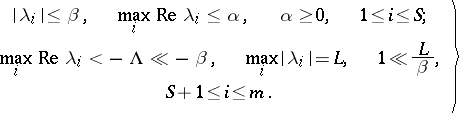
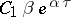 for
for  , where
, where 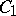 and
and 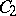 are certain constants. When
are certain constants. When 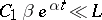 ,
, 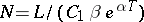 , condition b) is satisfied. The vector
, condition b) is satisfied. The vector 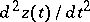 is bounded above if
is bounded above if 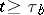 :
:
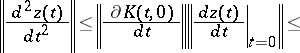
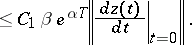
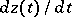 an algebraic interpolation polynomial of degree zero when
an algebraic interpolation polynomial of degree zero when 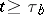 , with uniformly-distributed nodes, and to express the interpolation step in the form
, with uniformly-distributed nodes, and to express the interpolation step in the form 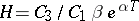 , where
, where 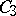 is some constant (see [1]) depending on the given error. On the other hand, use of Euler's polygonal method for (3) requires an upper bound on the size of the integration step on the entire interval of a solution of the system (see [1]):
is some constant (see [1]) depending on the given error. On the other hand, use of Euler's polygonal method for (3) requires an upper bound on the size of the integration step on the entire interval of a solution of the system (see [1]):
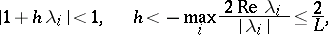
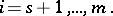
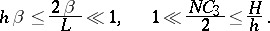
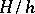 , which can be regarded as a qualitative measure of the stiffness of the system (3), attains values of order
, which can be regarded as a qualitative measure of the stiffness of the system (3), attains values of order 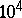 –
–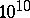 in many cases. The mathematical descriptions of dynamical processes and phenomena in physics, chemistry, biology, technology, and economics connected with the calculation of an ever larger number of factors raising the order of the differential systems, lead to an increase in stiffness. Stiff differential systems require special methods of solution.
in many cases. The mathematical descriptions of dynamical processes and phenomena in physics, chemistry, biology, technology, and economics connected with the calculation of an ever larger number of factors raising the order of the differential systems, lead to an increase in stiffness. Stiff differential systems require special methods of solution.
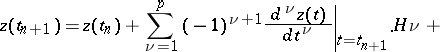
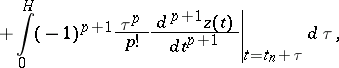
 is a positive integer,
is a positive integer, 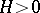 ,
, 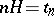 . For example, such methods are described in [9]:
. For example, such methods are described in [9]:
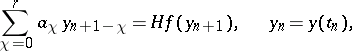
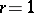 ,
, 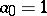 ,
, 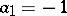 — the implicit polygonal method;
— the implicit polygonal method;
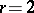 ,
, 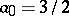 ,
, 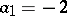 ,
, 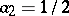 — the implicit
— the implicit  -nd order method;
-nd order method;
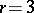 ,
, 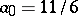 ,
, 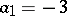 ,
, 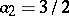 ,
, 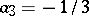 — the implicit
— the implicit  -rd order method;
-rd order method;
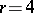 ,
, 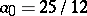 ,
, 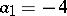 ,
, 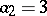 ,
, 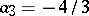 ,
, 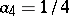 — the implicit 4th order method.
— the implicit 4th order method.
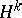 in the expansion (7) in powers of
in the expansion (7) in powers of 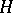 whose coefficient is the same as the corresponding coefficient in (6).
whose coefficient is the same as the corresponding coefficient in (6).

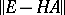 is non-singular for all
is non-singular for all  . The Lagrange–Sylvester formula can be used to represent the solution of (8) in the form
. The Lagrange–Sylvester formula can be used to represent the solution of (8) in the form
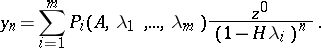
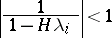
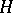 , and in (9) the components of the solution corresponding to the second group of eigenvalues (4) will be rapidly decreasing with increasing
, and in (9) the components of the solution corresponding to the second group of eigenvalues (4) will be rapidly decreasing with increasing  . The value of
. The value of 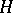 is restricted only by the requirements of the desired accuracy of the approximate solutions. The tendency to raise the order of linear multi-step methods leads to a definite contradiction to their stability (see [11]).
is restricted only by the requirements of the desired accuracy of the approximate solutions. The tendency to raise the order of linear multi-step methods leads to a definite contradiction to their stability (see [11]).
 -step method
-step method
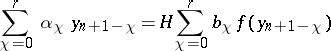
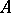 -stable if all solutions of (10) tend to zero as
-stable if all solutions of (10) tend to zero as 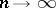 for a fixed positive
for a fixed positive 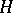 in the case when (10) is applied to the scalar equation
in the case when (10) is applied to the scalar equation
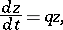
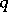 a complex constant with negative real part. An explicit
a complex constant with negative real part. An explicit  -step method cannot be
-step method cannot be 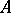 -stable. The order of a linear multi-step
-stable. The order of a linear multi-step 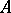 -stable method cannot exceed two. The smallest error constant
-stable method cannot exceed two. The smallest error constant 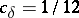 is obtained for the implicit trapezium method (see [11]):
is obtained for the implicit trapezium method (see [11]):
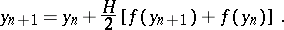
 -stability imposes less rigid restrictions on the methods, unlike
-stability imposes less rigid restrictions on the methods, unlike 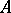 -stability. The
-stability. The  -step method (10) for fixed
-step method (10) for fixed 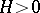 is said to be
is said to be 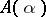 -stable if all solutions of (10) tend to zero as
-stable if all solutions of (10) tend to zero as 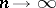 when (10) is applied to the equation (11), with
when (10) is applied to the equation (11), with 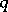 a complex constant in the set
a complex constant in the set
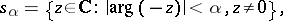
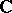 is the complex plane. An explicit
is the complex plane. An explicit  -step method cannot be
-step method cannot be 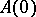 -stable. There exists only one
-stable. There exists only one 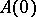 -stable
-stable  -step method of order
-step method of order 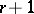 , namely (12). For
, namely (12). For 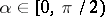 , there exist
, there exist 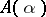 -stable methods of order
-stable methods of order  with
with 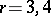 (see [13]).
(see [13]).
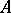 -stability is contained in the so-called definition of Gear (see [14]): (10) is said to be a stiffly-stable method if all solutions of (10) tend to zero as
-stability is contained in the so-called definition of Gear (see [14]): (10) is said to be a stiffly-stable method if all solutions of (10) tend to zero as 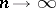 when (10) is applied to equation (11).
when (10) is applied to equation (11). 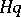 is a complex constant in
is a complex constant in 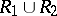 , where
, where
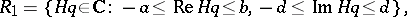
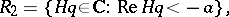
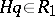 .
.
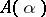 -stable. In these methods,
-stable. In these methods, 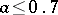 .
.
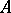 -stable and stiffly stable. For example, the
-stable and stiffly stable. For example, the  -nd order method
-nd order method
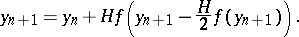
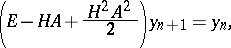
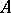 -stable. Similarly, for the
-stable. Similarly, for the  -rd order method
-rd order method
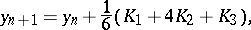
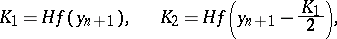
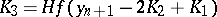
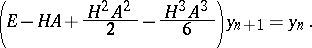
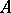 -stable and stiffly-stable methods of higher order are constructed in the same way. Methods (13) and (14), and those published in [5], are fundamentally different from the so-called implicit Runge–Kutta methods (see [16]), which have not become widely known because of their greater computational laboriousness. Application of implicit methods requires more computational effort at each step than is the case for explicit methods, but this is justified in stiff differential systems at the expense of a sharp increase in the size of the integration step. To solve (3), it is necessary to invert a matrix or to solve a system of linear equations. Here the problem of ill conditioning may arise, because the number of conditions on the matrix
-stable and stiffly-stable methods of higher order are constructed in the same way. Methods (13) and (14), and those published in [5], are fundamentally different from the so-called implicit Runge–Kutta methods (see [16]), which have not become widely known because of their greater computational laboriousness. Application of implicit methods requires more computational effort at each step than is the case for explicit methods, but this is justified in stiff differential systems at the expense of a sharp increase in the size of the integration step. To solve (3), it is necessary to invert a matrix or to solve a system of linear equations. Here the problem of ill conditioning may arise, because the number of conditions on the matrix 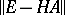 increases as
increases as 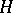 increases. In the general case of (1), at every integration step it is necessary to solve a non-linear system of equations for the vector
increases. In the general case of (1), at every integration step it is necessary to solve a non-linear system of equations for the vector 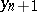 . It is common to use a modification of Newton's method with the initial condition calculated from an arbitrary extrapolation formula, using
. It is common to use a modification of Newton's method with the initial condition calculated from an arbitrary extrapolation formula, using 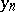 . The extrapolation method is then said to be a predictor and the implicit method a corrector. The method of simple iteration is inapplicable in stiff differential systems because of the large values of
. The extrapolation method is then said to be a predictor and the implicit method a corrector. The method of simple iteration is inapplicable in stiff differential systems because of the large values of 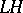 . Since Newton's method is applied in implicit schemes to solve the equations
. Since Newton's method is applied in implicit schemes to solve the equations 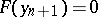 , and thus it is necessary to compute the Jacobi matrix of (1), this matrix is sometimes inserted directly into the formulas of the methods that also have the property of
, and thus it is necessary to compute the Jacobi matrix of (1), this matrix is sometimes inserted directly into the formulas of the methods that also have the property of 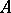 -stability for the solution of linear systems (see [12], [15]). Gear's procedure (Gear's method) is widely applied in the solution of stiff differential systems with automatic control of the error at each step, whence it alters the order of the method or the step size. Methods (7) are also used as correctors in Gear's procedure (see [9]). Another approach to the creation of methods for the integration of stiff systems of equations is connected with a calculation of the corresponding linear systems in the formulas of the solution methods (see [4]–[8], [10]). In the first articles in this direction, stiff systems of equations were discussed that had known eigenvalues for the matrix
-stability for the solution of linear systems (see [12], [15]). Gear's procedure (Gear's method) is widely applied in the solution of stiff differential systems with automatic control of the error at each step, whence it alters the order of the method or the step size. Methods (7) are also used as correctors in Gear's procedure (see [9]). Another approach to the creation of methods for the integration of stiff systems of equations is connected with a calculation of the corresponding linear systems in the formulas of the solution methods (see [4]–[8], [10]). In the first articles in this direction, stiff systems of equations were discussed that had known eigenvalues for the matrix 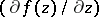 , according to which the matrix entries of the methods were constructed. Because of the difficulty of solving the eigenvalue problem, this direction was not developed for a considerable time. In [6], [7], [8], methods for constructing the matrix entries were proposed that did not require the solution of the eigenvalue problem for the matrix
, according to which the matrix entries of the methods were constructed. Because of the difficulty of solving the eigenvalue problem, this direction was not developed for a considerable time. In [6], [7], [8], methods for constructing the matrix entries were proposed that did not require the solution of the eigenvalue problem for the matrix 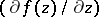 of the system (1). The methods in this direction can be constructed on the basis of the following equation (see [7]):
of the system (1). The methods in this direction can be constructed on the basis of the following equation (see [7]):
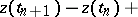

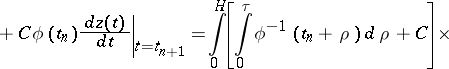

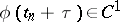 ,
, 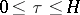 , is a non-singular (
, is a non-singular (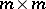 )-matrix and
)-matrix and 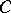 is a matrix not depending on
is a matrix not depending on  .
.
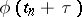 and
and 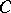 leads to difference equations corresponding to some method of numerical integration if the right-hand side of (15) is disregarded. For
leads to difference equations corresponding to some method of numerical integration if the right-hand side of (15) is disregarded. For 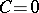 , explicit methods are obtained, and for
, explicit methods are obtained, and for 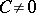 — implicit methods. Suppose that
— implicit methods. Suppose that 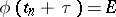 . Then the implicit polygonal method (7) corresponds to
. Then the implicit polygonal method (7) corresponds to 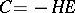 ; the trapezium method (12) to
; the trapezium method (12) to 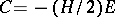 ; and the explicit polygonal method to
; and the explicit polygonal method to 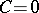 . When
. When 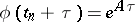 , where
, where 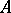 is a constant (
is a constant (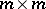 )-matrix, a generalized polygonal method is obtained (see [7]):
)-matrix, a generalized polygonal method is obtained (see [7]):

 . Method (16) gives an exact solution of the system of equations
. Method (16) gives an exact solution of the system of equations
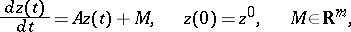
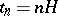 . If the matrix
. If the matrix
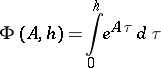
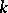 iterations of the recurrence relation
iterations of the recurrence relation
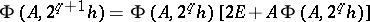
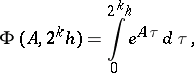
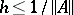 , it is appropriate to use the approximation formula
, it is appropriate to use the approximation formula
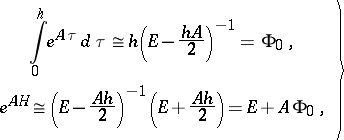
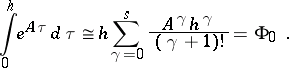
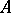 has complex eigenvalues with small real part. If the domain
has complex eigenvalues with small real part. If the domain 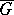 of existence of the solutions is closed, convex in
of existence of the solutions is closed, convex in  , and if the approximate solutions belong to this domain, then the error in (16) satisfies the following difference equation (see [7]):
, and if the approximate solutions belong to this domain, then the error in (16) satisfies the following difference equation (see [7]):

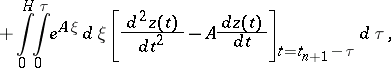
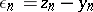 and
and  ,
, 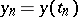 are solutions of (1) and (16), respectively. Let
are solutions of (1) and (16), respectively. Let  be the norm of the vector (the norms of the matrices are subordinated to this vector norm), and suppose that the following inequalities are satisfied in
be the norm of the vector (the norms of the matrices are subordinated to this vector norm), and suppose that the following inequalities are satisfied in 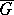 :
:
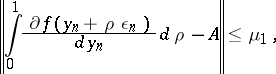
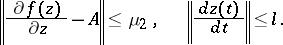
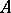 :
:
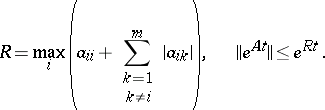
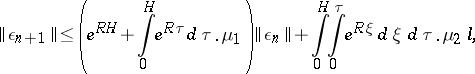

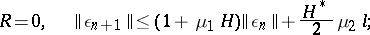
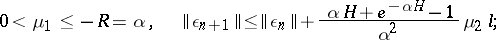
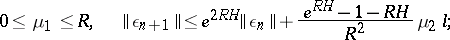
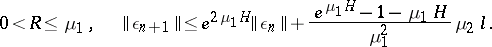
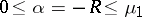 , the error
, the error 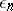 can be estimated on the assumption that
can be estimated on the assumption that 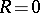 . Other vector norms are possible in the estimates, with corresponding matrix norms and logarithmic norms (see [3]). These estimates prove that in the solution of (1), the integration step
. Other vector norms are possible in the estimates, with corresponding matrix norms and logarithmic norms (see [3]). These estimates prove that in the solution of (1), the integration step 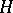 can be taken significantly larger than in classical methods. The matrix
can be taken significantly larger than in classical methods. The matrix 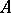 must be chosen in such a way that all its entries are close to those of the Jacobi matrix of the system (1). In the boundary layer, when the variables change rapidly, by estimating
must be chosen in such a way that all its entries are close to those of the Jacobi matrix of the system (1). In the boundary layer, when the variables change rapidly, by estimating 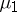 ,
, 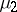 ,
, 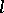 , and
, and 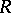 roughly for the approximate solution, it is possible to change
roughly for the approximate solution, it is possible to change 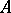 so as to obtain the necessary accuracy. Since the variables in (1) change slowly across the boundary layer, it often turns out that one matrix
so as to obtain the necessary accuracy. Since the variables in (1) change slowly across the boundary layer, it often turns out that one matrix 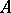 is sufficient to compute all solutions when
is sufficient to compute all solutions when 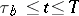 . The checking of the accuracy can be accomplished by using Runge's rule (see [1]).
. The checking of the accuracy can be accomplished by using Runge's rule (see [1]).
 -th order method must be exact for the integration of algebraic polynomials of degree
-th order method must be exact for the integration of algebraic polynomials of degree 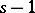 when
when 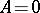 ; and 2) a method of arbitrary order must be exact for the solution of (17).
; and 2) a method of arbitrary order must be exact for the solution of (17).
 -nd order method has the form:
-nd order method has the form:
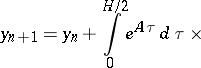
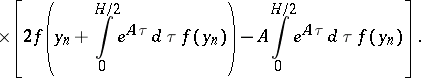
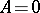 , these methods become formulas of Runge–Kutta or Adams type. In the approximation to integrals of
, these methods become formulas of Runge–Kutta or Adams type. In the approximation to integrals of 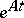 by fractional-linear matrix polynomials in
by fractional-linear matrix polynomials in 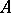 , taking into account the non-singularity of the corresponding matrices, the methods for systems go over to the explicit formulas of the corresponding implicit methods obtained after iteration by Newton's method. The following is an implicit
, taking into account the non-singularity of the corresponding matrices, the methods for systems go over to the explicit formulas of the corresponding implicit methods obtained after iteration by Newton's method. The following is an implicit 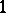 -st order method for systems:
-st order method for systems:
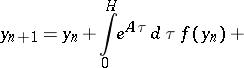
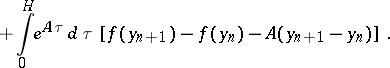
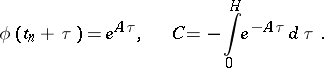
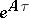 in (21) is calculated according to (18) with the initial condition (20). A method of correction of this integral in the course of solving has been investigated (see ).
in (21) is calculated according to (18) with the initial condition (20). A method of correction of this integral in the course of solving has been investigated (see ).