Stieltjes integral
A generalization of the concept of the Riemann integral, realizing the notion of integrating a function 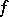 with respect to another function
with respect to another function  . Let two functions
. Let two functions 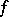 and
and  be defined and bounded on
be defined and bounded on  and let
and let 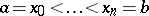 . A sum of the form
. A sum of the form
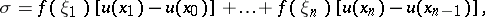 | (1) |
where 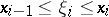 ,
, 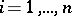 , is called a Stieltjes integral sum. A number
, is called a Stieltjes integral sum. A number 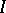 is called the limit of the integral sums (1) when
is called the limit of the integral sums (1) when 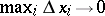 if for each
if for each 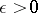 there is a
there is a 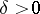 such that if
such that if 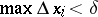 , the inequality
, the inequality 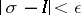 holds. If the limit
holds. If the limit 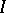 exists when
exists when 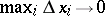 and is finite, then the function
and is finite, then the function 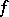 is said to be integrable with respect to the function
is said to be integrable with respect to the function  over
over 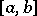 , and the limit is called the Stieltjes integral (or the Riemann–Stieltjes integral) of
, and the limit is called the Stieltjes integral (or the Riemann–Stieltjes integral) of 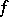 with respect to
with respect to  , and is denoted by
, and is denoted by
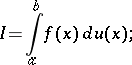 | (2) |
the function  is said to be the integrating function. Th.J. Stieltjes [1] hit upon the idea of such an integral when studying the positive "distribution of masses" on a straight line defined by an increasing function
is said to be the integrating function. Th.J. Stieltjes [1] hit upon the idea of such an integral when studying the positive "distribution of masses" on a straight line defined by an increasing function  , the points of discontinuity of which correspond to masses that are "concentrated at one point" .
, the points of discontinuity of which correspond to masses that are "concentrated at one point" .
The Riemann integral is a particular case of the Stieltjes integral, when a function 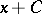 , where
, where 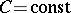 , is taken as the integrating function
, is taken as the integrating function  .
.
When the integrating function  increases monotonically, the upper and lower Darboux–Stieltjes sums are studied:
increases monotonically, the upper and lower Darboux–Stieltjes sums are studied:
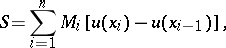 | (3) |
 |
where 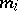 and
and 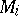 are the greatest lower and least upper bounds of
are the greatest lower and least upper bounds of  on
on 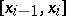 .
.
For a Stieltjes integral to exists, it is sufficient for one of the following conditions to be fulfilled:
1) the function 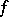 is continuous on
is continuous on 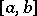 , while the function
, while the function  is of bounded variation on
is of bounded variation on 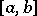 ;
;
2) the function 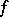 is Riemann integrable on
is Riemann integrable on 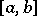 , while the function
, while the function  satisfies a Lipschitz condition on
satisfies a Lipschitz condition on 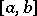 , i.e.
, i.e. 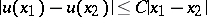 , where
, where  , for any
, for any 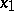 and
and 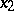 from
from 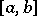 ;
;
3) the function  is Riemann integrable on
is Riemann integrable on 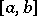 , while the function
, while the function  can be represented on
can be represented on 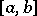 as an integral with a variable upper bound,
as an integral with a variable upper bound,
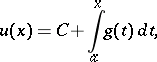 |
where 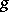 is absolutely integrable over
is absolutely integrable over 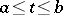 .
.
When condition 3) is fulfilled, the integral (2) reduces to a Lebesgue integral by the formula
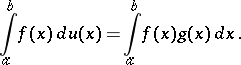 | (4) |
(The right-hand side is a Riemann integral if 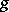 is Riemann integrable.) In particular, (4) holds if
is Riemann integrable.) In particular, (4) holds if  has a bounded and Riemann-integrable derivative
has a bounded and Riemann-integrable derivative 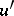 on
on  ; in this case
; in this case 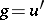 .
.
If  is integrable with respect to
is integrable with respect to 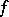 over
over 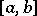 , then
, then 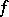 is also integrable with respect to
is also integrable with respect to  over
over 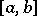 . This statement leads to a number of further conditions on the existence of Stieltjes integrals.
. This statement leads to a number of further conditions on the existence of Stieltjes integrals.
The Stieltjes integral has the property of linearity relative to both the integrand and the integrating function (given the condition that every one of the Stieltjes integrals on the right-hand side exists):
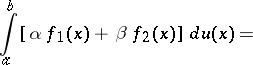 |
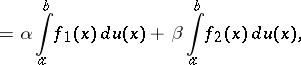 |
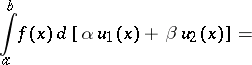 |
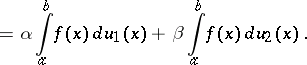 |
Generally speaking, Stieltjes integrals do not possess the property of additivity: The existence of 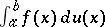 does not follow from the existence of both the integrals
does not follow from the existence of both the integrals 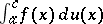 and
and  (the converse is, instead, true if
(the converse is, instead, true if 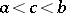 ).
).
If 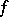 is bounded on
is bounded on 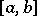 ,
, 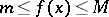 , and
, and  increases monotonically on
increases monotonically on 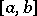 , then there exists a
, then there exists a 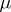 satisfying the inequality
satisfying the inequality  , such that the mean-value formula
, such that the mean-value formula
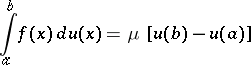 | (5) |
holds for a Stieltjes integral. In particular, if 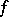 is continuous on
is continuous on 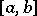 , then there exists a point
, then there exists a point 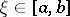 such that
such that 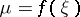 .
.
A Stieltjes integral  , where
, where  is of bounded variation, provides the general form of a continuous linear functional
is of bounded variation, provides the general form of a continuous linear functional 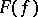 on the space of continuous functions on
on the space of continuous functions on 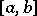 (Riesz' theorem).
(Riesz' theorem).
When the function  is of bounded variation, the value of the Stieltjes integral coincides with the value of the corresponding Lebesgue–Stieltjes integral.
is of bounded variation, the value of the Stieltjes integral coincides with the value of the corresponding Lebesgue–Stieltjes integral.
References
| [1] | Th.J. Stieltjes, "Recherches sur les fractions continues" C.R. Acad. Sci. Paris , 118 (1894) pp. 1401–1403 |
| [2] | V.I. Smirnov, "A course of higher mathematics" , 5 , Addison-Wesley (1964) (Translated from Russian) |
| [3] | V.I. Glivenko, "The Stieltjes integral" , Moscow-Leningrad (1936) (In Russian) |
Comments
References
| [a1] | K.A. Ross, "Elementary analysis: The theory of calculus" , Springer (1980) |
| [a2] | W. Rudin, "Principles of mathematical analysis" , McGraw-Hill (1976) pp. 75–78 |
| [a3] | T.M. Apostol, "Mathematical analysis" , Addison-Wesley (1974) |
Stieltjes integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stieltjes_integral&oldid=17367