Stiefel number
A characteristic number of a closed manifold taking values in  , the integers modulo 2. Let
, the integers modulo 2. Let  be an arbitrary stable characteristic class, and let
be an arbitrary stable characteristic class, and let  be a closed manifold. The residue modulo 2 defined by
be a closed manifold. The residue modulo 2 defined by
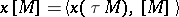 |
is called the Stiefel number (or Stiefel–Whitney number) of  corresponding to the class
corresponding to the class  . Here
. Here  is the tangent bundle of
is the tangent bundle of  , and
, and  is the fundamental class. For
is the fundamental class. For  -dimensional manifolds, the Stiefel number depends only on the
-dimensional manifolds, the Stiefel number depends only on the  -th homogeneous component of the class
-th homogeneous component of the class  . The group
. The group 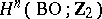 is isomorphic to a vector space over the field
is isomorphic to a vector space over the field 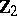 whose basis is in one-to-one correspondence with the set of all partitions
whose basis is in one-to-one correspondence with the set of all partitions 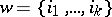 of the number
of the number  , i.e. tuples
, i.e. tuples 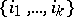 of non-negative integers such that
of non-negative integers such that 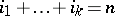 . The classes
. The classes 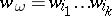 would be a natural choice for a basis of
would be a natural choice for a basis of 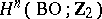 . Thus, to characterize a manifold by its Stiefel numbers it is sufficient to consider the classes
. Thus, to characterize a manifold by its Stiefel numbers it is sufficient to consider the classes 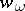 , where
, where 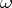 is a partition of the dimension of the manifold.
is a partition of the dimension of the manifold.
Bordant manifolds have the same Stiefel numbers, since each characteristic class  determines a homomorphism
determines a homomorphism 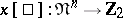 , where
, where 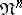 is the group of classes of bordant non-oriented
is the group of classes of bordant non-oriented  -dimensional manifolds. If for two closed manifolds
-dimensional manifolds. If for two closed manifolds 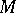 ,
, 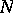 the equality
the equality  holds for all partitions
holds for all partitions 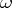 of
of  , then the manifolds
, then the manifolds  and
and 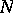 are bordant (Thom's theorem).
are bordant (Thom's theorem).
Let 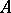 be the vector space
be the vector space 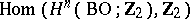 over the field
over the field 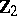 . Let
. Let  be the basis in
be the basis in 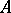 dual to the basis
dual to the basis 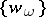 in
in 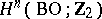 ,
, 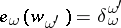 , here
, here  are partitions of
are partitions of  ; and let a mapping
; and let a mapping 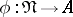 be defined by
be defined by  . The mapping
. The mapping  is monomorphic, and for a complete description of the group
is monomorphic, and for a complete description of the group 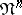 by the Stiefel numbers it is necessary to find its image. This problem is analogous to the Milnor–Hirzebruch problem for Chern classes (cf. Chern class). For a closed manifold
by the Stiefel numbers it is necessary to find its image. This problem is analogous to the Milnor–Hirzebruch problem for Chern classes (cf. Chern class). For a closed manifold 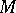 , let
, let 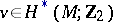 be the so-called Wu class, uniquely defined by
be the so-called Wu class, uniquely defined by 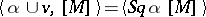 , which should hold for all
, which should hold for all 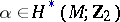 . Then
. Then 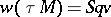 , where
, where 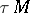 is the tangent bundle to
is the tangent bundle to 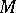 (Wu's theorem).
(Wu's theorem).
This theorem implies that the Wu class can be defined as a characteristic class: Let
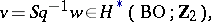 |
where 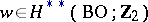 is the complete Stiefel–Whitney class and
is the complete Stiefel–Whitney class and 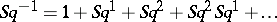 is the cohomology operation inverse to the complete Steenrod square
is the cohomology operation inverse to the complete Steenrod square 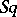 . Let
. Let 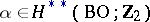 be an arbitrary characteristic class. Then for any closed manifold the numbers
be an arbitrary characteristic class. Then for any closed manifold the numbers 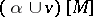 and
and 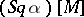 coincide. Thus, an element
coincide. Thus, an element 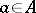 ,
, 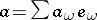 can be in the image of the mapping
can be in the image of the mapping 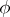 only if
only if 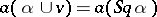 holds for all
holds for all 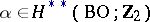 . For a homomorphism
. For a homomorphism 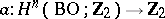 there exists a manifold
there exists a manifold 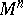 such that
such that 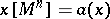 for all
for all  if and only if
if and only if 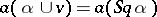 for all
for all 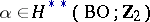 (Dold's theorem).
(Dold's theorem).
For references, see Stiefel–Whitney class.
Comments
As is customary 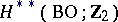 denotes the direct product of the cohomology groups
denotes the direct product of the cohomology groups  of the classifying space
of the classifying space 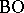 , while
, while 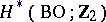 is the direct sum.
is the direct sum.
Stiefel number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stiefel_number&oldid=11762