Difference between revisions of "Stereographic projection"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | The correspondence between the points of a sphere and a plane, obtained in the following way: From a point | + | {{TEX|done}} |
| + | The correspondence between the points of a sphere and a plane, obtained in the following way: From a point $S$ on the sphere (the centre of the stereographic projection) the other points of the sphere are projected by rays onto a plane perpendicular to the radius $SO$ of the sphere (in the figure, this plane is equatorial, but it could be drawn through the end $S_1$ of the diameter $SS_1$). Every point $M$ on the sphere goes into a definite point $M'$ on the plane. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s087750a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/s087750a.gif" /> | ||
| Line 5: | Line 6: | ||
Figure: s087750a | Figure: s087750a | ||
| − | If one assumes that the point at infinity of the plane corresponds to the point | + | If one assumes that the point at infinity of the plane corresponds to the point $S$, then the correspondence between the points of the sphere and the plane will be a one-to-one correspondence. The basic properties of stereographic projection are: |
1) circles on the plane correspond to circles on the sphere, while circles passing through the point at infinity, i.e. straight lines, correspond to circles passing through the centre of the stereographic projection; | 1) circles on the plane correspond to circles on the sphere, while circles passing through the point at infinity, i.e. straight lines, correspond to circles passing through the centre of the stereographic projection; | ||
| Line 11: | Line 12: | ||
2) angles between lines are preserved under stereographic projection. | 2) angles between lines are preserved under stereographic projection. | ||
| − | If a point of the three-dimensional space is defined by the homogeneous coordinates | + | If a point of the three-dimensional space is defined by the homogeneous coordinates $x_1,x_2,x_3,x_4$ and the equation of the sphere is taken to be $x_1^2+x_2^2+x_3^2-x_4^2=0$, while a point of the plane is defined by the Cartesian coordinates $\xi,\eta$, then the connection between the points of the sphere and the plane is defined by the formulas |
| − | + | $$\sigma x_1=\xi,\quad \sigma x_2=\eta,$$ | |
| − | + | $$\sigma x_3=\frac{1-(\xi^2-\eta^2)}{2},\quad\sigma x_4=\frac{1+(\xi^2+\eta^2)}{2}.$$ | |
| − | The coordinates | + | The coordinates $x_1,x_2,x_3,x_4$ can be considered as coordinates of points on the plane ([[Tetracyclic coordinates|tetracyclic coordinates]]). |
Stereographic projection establishes a correspondence not only between the points of the sphere and the plane, but also between points outside the sphere and circles on the plane. For a point outside the sphere, the polar plane intersects the sphere along a circle. Under stereographic projection, this circle is transformed to a circle on the plane, which is also considered as the stereographic image of the point outside the sphere onto the plane. The coordinates of a point of the three-dimensional space are considered as tetracyclic coordinates of the circle on the plane. Under stereographic projection, the points inside the sphere have corresponding imaginary images on the plane. | Stereographic projection establishes a correspondence not only between the points of the sphere and the plane, but also between points outside the sphere and circles on the plane. For a point outside the sphere, the polar plane intersects the sphere along a circle. Under stereographic projection, this circle is transformed to a circle on the plane, which is also considered as the stereographic image of the point outside the sphere onto the plane. The coordinates of a point of the three-dimensional space are considered as tetracyclic coordinates of the circle on the plane. Under stereographic projection, the points inside the sphere have corresponding imaginary images on the plane. | ||
| Line 23: | Line 24: | ||
A stereographic projection can also be studied more generally: instead of a sphere, any surface of the second order can be used. This projection is also called a Hesse mapping. | A stereographic projection can also be studied more generally: instead of a sphere, any surface of the second order can be used. This projection is also called a Hesse mapping. | ||
| − | In the multi-dimensional case, a stereographic projection is a projection of points of the Euclidean space | + | In the multi-dimensional case, a stereographic projection is a projection of points of the Euclidean space $E_{n+1}$ onto the space $E_n$ complemented by one point at infinity, from a point $P$ of the sphere $S_n$ in $E_{n+1}$, where $P$ does not lie in $E_n$. All arguments and formulas are analogous to those mentioned above. |
Using stereographic projection, the extended complex plane is conformally mapped one-to-one onto the [[Riemann sphere|Riemann sphere]]. | Using stereographic projection, the extended complex plane is conformally mapped one-to-one onto the [[Riemann sphere|Riemann sphere]]. | ||
Revision as of 15:50, 22 July 2014
The correspondence between the points of a sphere and a plane, obtained in the following way: From a point $S$ on the sphere (the centre of the stereographic projection) the other points of the sphere are projected by rays onto a plane perpendicular to the radius $SO$ of the sphere (in the figure, this plane is equatorial, but it could be drawn through the end $S_1$ of the diameter $SS_1$). Every point $M$ on the sphere goes into a definite point $M'$ on the plane.
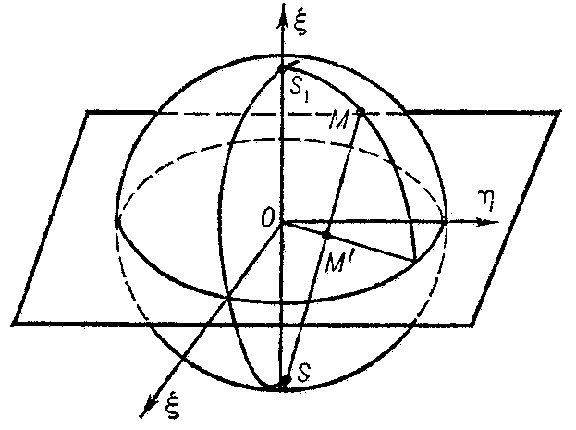
Figure: s087750a
If one assumes that the point at infinity of the plane corresponds to the point $S$, then the correspondence between the points of the sphere and the plane will be a one-to-one correspondence. The basic properties of stereographic projection are:
1) circles on the plane correspond to circles on the sphere, while circles passing through the point at infinity, i.e. straight lines, correspond to circles passing through the centre of the stereographic projection;
2) angles between lines are preserved under stereographic projection.
If a point of the three-dimensional space is defined by the homogeneous coordinates $x_1,x_2,x_3,x_4$ and the equation of the sphere is taken to be $x_1^2+x_2^2+x_3^2-x_4^2=0$, while a point of the plane is defined by the Cartesian coordinates $\xi,\eta$, then the connection between the points of the sphere and the plane is defined by the formulas
$$\sigma x_1=\xi,\quad \sigma x_2=\eta,$$
$$\sigma x_3=\frac{1-(\xi^2-\eta^2)}{2},\quad\sigma x_4=\frac{1+(\xi^2+\eta^2)}{2}.$$
The coordinates $x_1,x_2,x_3,x_4$ can be considered as coordinates of points on the plane (tetracyclic coordinates).
Stereographic projection establishes a correspondence not only between the points of the sphere and the plane, but also between points outside the sphere and circles on the plane. For a point outside the sphere, the polar plane intersects the sphere along a circle. Under stereographic projection, this circle is transformed to a circle on the plane, which is also considered as the stereographic image of the point outside the sphere onto the plane. The coordinates of a point of the three-dimensional space are considered as tetracyclic coordinates of the circle on the plane. Under stereographic projection, the points inside the sphere have corresponding imaginary images on the plane.
A stereographic projection can also be studied more generally: instead of a sphere, any surface of the second order can be used. This projection is also called a Hesse mapping.
In the multi-dimensional case, a stereographic projection is a projection of points of the Euclidean space $E_{n+1}$ onto the space $E_n$ complemented by one point at infinity, from a point $P$ of the sphere $S_n$ in $E_{n+1}$, where $P$ does not lie in $E_n$. All arguments and formulas are analogous to those mentioned above.
Using stereographic projection, the extended complex plane is conformally mapped one-to-one onto the Riemann sphere.
References
| [1] | F. Klein, "Vorlesungen über höhere Geometrie" , Springer (1926) |
| [2] | W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einstein's Relativitätstheorie" , 3. Differentialgeometrie der Kreisen und Kugeln , Springer (1929) |
| [3] | G.B. Bushmanova, "Elements of conformal geometry" , Kazan' (1972) (In Russian) |
Comments
References
| [a1] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) |
| [a2] | D.J. Struik, "Differential geometry" , Addison-Wesley (1957) |
| [a3] | C.E. Weatherburn, "Differential geometry" , 1 , Cambridge Univ. Press (1961) |
| [a4] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) |
| [a5] | D. Hilbert, S.E. Cohn-Vossen, "Geometry and the imagination" , Chelsea (1952) (Translated from German) |
Stereographic projection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stereographic_projection&oldid=16306