Steklov function
for an integrable function 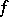 on a bounded segment
on a bounded segment 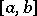
The function
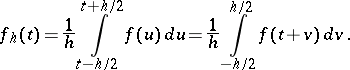 | (*) |
Functions of the form (*), as well as the iteratively defined functions
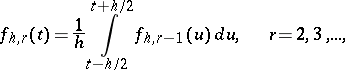 |
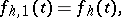 |
were first introduced in 1907 by V.A. Steklov (see [1]) in solving the problem of expanding a given function into a series of eigenfunctions. The Steklov function 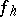 has derivative
has derivative
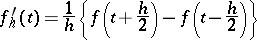 |
almost everywhere. If 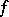 is uniformly continuous on the whole real axis, then
is uniformly continuous on the whole real axis, then
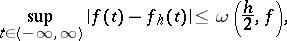 |
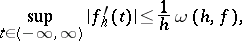 |
where  is the modulus of continuity of
is the modulus of continuity of 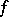 . Similar inequalities hold in the metric of
. Similar inequalities hold in the metric of 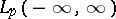 , provided
, provided 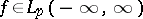 .
.
References
| [1] | V.A. Steklov, "On the asymptotic representation of certain functions defined by a linear differential equation of the second order, and their application to the problem of expanding an arbitrary function into a series of these functions" , Khar'kov (1957) (In Russian) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
Comments
Steklov's fundamental paper was first published in French (1907) in the "Communications of the Mathematical Society of Kharkov" ; [1] is the Russian translation, together with additional comments by N.S. Landkof.
References
| [a1] | E.W. Cheney, "Introduction to approximation theory" , Chelsea, reprint (1982) |
| [a2] | M.W. Müller, "Approximationstheorie" , Akad. Verlagsgesellschaft (1978) |
Steklov function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steklov_function&oldid=17657