Stein manifold
holomorphically-complete manifold
A paracompact complex analytic manifold  with the following properties:
with the following properties:
1) for any compact set  the set
the set
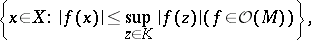 |
where  is the algebra of holomorphic functions on
is the algebra of holomorphic functions on  , is compact (holomorphic convexity);
, is compact (holomorphic convexity);
2) for any two different points  there is a function
there is a function  such that
such that  (holomorphic separability);
(holomorphic separability);
3) in a neighbourhood of any point there is a holomorphic chart whose coordinate functions belong to  .
.
The requirement of holomorphic convexity can be replaced by the following one: For any sequence  without limit points there is a function
without limit points there is a function 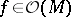 such that
such that 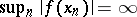 .
.
The class of Stein manifolds was introduced by K. Stein [1] as a natural generalization of the notion of a domain of holomorphy in 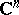 . Any closed analytic submanifold in
. Any closed analytic submanifold in  is a Stein manifold; conversely, any
is a Stein manifold; conversely, any  -dimensional Stein manifold has a proper holomorphic imbedding in
-dimensional Stein manifold has a proper holomorphic imbedding in 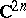 (cf. Proper morphism). Any non-compact Riemann surface is a Stein manifold. The direct generalization of a Stein manifold is a Stein space.
(cf. Proper morphism). Any non-compact Riemann surface is a Stein manifold. The direct generalization of a Stein manifold is a Stein space.
See also the references to Stein space.
References
| [1] | K. Stein, "Analytische Funktionen mehrerer komplexer Veränderlichen zu vorgegebenen Periodizitätsmoduln und das zweite Cousinsche Problem" Math. Ann. , 123 (1951) pp. 201–222 |
Stein manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stein_manifold&oldid=18400