Steenrod duality
An isomorphism between the 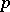 -dimensional homology group of a compact subset
-dimensional homology group of a compact subset 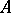 of the sphere
of the sphere 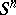 and the
and the 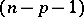 -dimensional cohomology group of the complement (the homology and cohomology groups are the reduced ones). The problem was examined by N. Steenrod [1]. When
-dimensional cohomology group of the complement (the homology and cohomology groups are the reduced ones). The problem was examined by N. Steenrod [1]. When 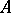 is an open or closed subpolyhedron, the same isomorphism is known as Alexander duality, and for any open subset
is an open or closed subpolyhedron, the same isomorphism is known as Alexander duality, and for any open subset 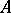 as Pontryagin duality. The isomorphism
as Pontryagin duality. The isomorphism
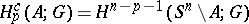 |
also holds for an arbitrary subset 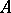 (Sitnikov duality); here the
(Sitnikov duality); here the 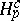 are the Steenrod–Sitnikov homology groups with compact supports, and the
are the Steenrod–Sitnikov homology groups with compact supports, and the 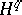 are the Aleksandrov–Čech cohomology groups. Alexander–Pontryagin–Steenrod–Sitnikov duality is a simple consequence of Poincaré–Lefschetz duality and of the exact sequence of a pair. It is correct not only for
are the Aleksandrov–Čech cohomology groups. Alexander–Pontryagin–Steenrod–Sitnikov duality is a simple consequence of Poincaré–Lefschetz duality and of the exact sequence of a pair. It is correct not only for 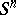 , but also for any manifold which is acyclic in dimensions
, but also for any manifold which is acyclic in dimensions 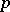 and
and 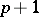 .
.
References
| [1] | N. Steenrod, "Regular cycles on compact metric spaces" Ann. of Math. , 41 (1940) pp. 833–851 |
| [2] | K.A. Sitnikov, "The duality law for non-closed sets" Dokl. Akad. Nauk SSSR , 81 (1951) pp. 359–362 (In Russian) |
| [3] | E.G. Sklyarenko, "On homology theory associated with the Aleksandrov–Čech cohomology" Russian Math. Surveys , 34 : 6 (1979) pp. 103–137 Uspekhi Mat. Nauk , 34 : 6 (1979) pp. 90–118 |
| [4] | W.S. Massey, "Notes on homology and cohomology theory" , Yale Univ. Press (1964) |
Steenrod duality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod_duality&oldid=17482