Steenrod-Sitnikov homology
A homology theory  supposed to be defined on the category of pairs of compact metric (i.e., metrizable) spaces
supposed to be defined on the category of pairs of compact metric (i.e., metrizable) spaces  , satisfying all Steenrod–Eilenberg axioms (in the case of generalized Steenrod–Sitnikov homology, without a dimension axiom) together with a strong excision axiom (i.e.
, satisfying all Steenrod–Eilenberg axioms (in the case of generalized Steenrod–Sitnikov homology, without a dimension axiom) together with a strong excision axiom (i.e.  induces an isomorphism in homology).
induces an isomorphism in homology).
For an ordinary Steenrod–Sitnikov homology theory  (
( an Abelian group) J. Milnor [a3] established the following axiomatic characterization: An ordinary homology theory
an Abelian group) J. Milnor [a3] established the following axiomatic characterization: An ordinary homology theory  on
on  satisfying the Eilenberg–Steenrod axioms (with strong excision and dimension axiom) and in addition the cluster (or strong wedge) axiom is isomorphic (as a homology theory) to
satisfying the Eilenberg–Steenrod axioms (with strong excision and dimension axiom) and in addition the cluster (or strong wedge) axiom is isomorphic (as a homology theory) to  .
.
Let  ,
, 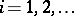 , be a family of based spaces in
, be a family of based spaces in 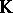 ; then the cluster
; then the cluster 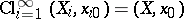 is the wedge of the
is the wedge of the 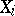 , equipped with the strong topology (a neighbourhood of the basepoint
, equipped with the strong topology (a neighbourhood of the basepoint 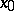 contains almost all
contains almost all 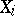 or, alternatively,
or, alternatively, 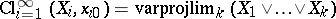 ). The projection
). The projection 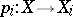 induces a mapping
induces a mapping
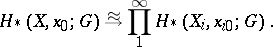 | (a1) |
The cluster axiom requires that (a1) be an isomorphism.
The cluster axiom turns out to be some kind of continuity axiom: A homology theory 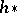 is continuous whenever there is a natural isomorphism
is continuous whenever there is a natural isomorphism
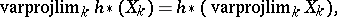 | (a2) |
i.e. the functor  commutes with inverse limits. S. Eilenberg and N. Steenrod [a2] discovered that there is a conflict between (a2) and the exactness axiom, so that no homology theory can be continuous. However, the cluster axiom reveals itself as a special case of (a2): One has
commutes with inverse limits. S. Eilenberg and N. Steenrod [a2] discovered that there is a conflict between (a2) and the exactness axiom, so that no homology theory can be continuous. However, the cluster axiom reveals itself as a special case of (a2): One has
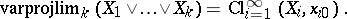 |
and
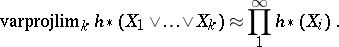 |
Milnor's uniqueness theorem admits an extension for generalized homology theories [a1]: A homology theory  on
on  satisfying the Milnor axioms (now without a dimension axiom) is, up to an isomorphism of homology theories, uniquely determined by its restriction to the category of compact absolute neighbourhood retracts
satisfying the Milnor axioms (now without a dimension axiom) is, up to an isomorphism of homology theories, uniquely determined by its restriction to the category of compact absolute neighbourhood retracts  (or polyhedra or CW-spaces). Moreover, every homology theory
(or polyhedra or CW-spaces). Moreover, every homology theory 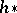 on
on  admits a unique extension
admits a unique extension  over
over 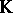 as a Steenrod–Sitnikov homology theory. If
as a Steenrod–Sitnikov homology theory. If 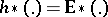 (the homology theory with coefficients in a spectrum,
(the homology theory with coefficients in a spectrum,  ) (cf. also Spectrum of spaces), then
) (cf. also Spectrum of spaces), then 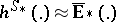 is uniquely determined by the spectrum
is uniquely determined by the spectrum 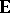 .
.
It turns out [a1] that 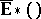 is constructed like
is constructed like 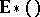 , but with replacing continuous mappings by strong shape mappings. So, Steenrod–Sitnikov homology is defined on a strong shape category (cf. Strong shape theory).
, but with replacing continuous mappings by strong shape mappings. So, Steenrod–Sitnikov homology is defined on a strong shape category (cf. Strong shape theory).
Steenrod–Sitnikov homology appears as the appropriate tool for handling geometric problems in 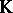 . This pertains to Alexander duality in its most modern form, dealing with homology and cohomology with coefficients in a spectrum, to
. This pertains to Alexander duality in its most modern form, dealing with homology and cohomology with coefficients in a spectrum, to 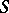 -duality, as well as to dimension theory of subspaces of
-duality, as well as to dimension theory of subspaces of 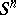 .
.
Ordinary Steenrod–Sitnikov homology appeared for the first time in [a6] as a tool for Alexander duality. In the 1950s, K. Sitnikov rediscovered 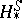 by using a different definition [a4], [a5], without knowing about [a6], and verified an Alexander duality theorem for arbitrary
by using a different definition [a4], [a5], without knowing about [a6], and verified an Alexander duality theorem for arbitrary 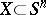 by using this kind of homology with compact support.
by using this kind of homology with compact support.
As official opponent in Sitnikov's doctoral dissertation, G.S. Chogoshvili pointed out that the homology groups of Sitnikov and Steenrod agree.
Sitnikov's definition of 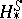 is modelled after the classical definition of Vietoris homology: A Vietoris cycle
is modelled after the classical definition of Vietoris homology: A Vietoris cycle  on a space
on a space 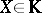 consists of a sequence of
consists of a sequence of 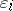 -cycles,
-cycles, 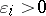 (i.e. each
(i.e. each 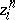 is a cycle with simplices with vertices in
is a cycle with simplices with vertices in 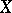 of maximal diameter
of maximal diameter 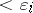 ), with
), with 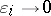 , such that
, such that 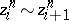 by some
by some 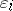 -chain
-chain 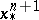 :
:
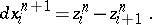 |
A Sitnikov-cycle 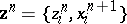 specifies the chains
specifies the chains 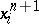 . So, two Sitnikov cycles
. So, two Sitnikov cycles
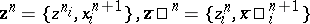 |
give rise to the same Vietoris cycle but eventually to different Sitnikov homology classes.
There have been attempts to extend Steenrod–Sitnikov homology to more general topological spaces, leading to what is called strong homology. This was initiated for ordinary homology theories by S. Mardešić and Ju. Lisica. There is an analogous axiomatic characterization of strong homology, where one has to replace the cluster axiom by a continuity axiom on the chain level (the c-continuity of a homology theory).
References
| [a1] | F.W. Bauer, "Extensions of generalized homology theories" Pacific J. Math. , 128 : 1 (1987) pp. 25–61 |
| [a2] | S. Eilenberg, N. Steenrod, "Foundations of algebraic topology" , Princeton Math. Ser. , 15 , Princeton Univ. Press (1952) |
| [a3] | J. Milnor, "On the Steenrod homology theory" , Berkeley (unpublished) |
| [a4] | K. Sitnikov, "Combinatorial topology of non-closed sets I" Mat. Sb. , 84 : 76 (1954) pp. 3–54 (In Russian) |
| [a5] | K. Sitnikov, "Combinatorial topology of non-closed sets I–II" Mat. Sb. , 37 : 79 (1955) pp. 355–434 (In Russian) |
| [a6] | N. Steenrod, "Regular cycles of compact metric spaces" Amer. J. Math. , 41 (1940) pp. 833–85 |
Steenrod-Sitnikov homology. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod-Sitnikov_homology&oldid=17110