Statistics
A term used in mathematical statistics as a name for functions of the results of observations.
Let a random variable  take values in the sample space
take values in the sample space  . Any
. Any  -measurable mapping
-measurable mapping  from
from  onto a measurable space
onto a measurable space  is then called a statistic, and the probability distribution of the statistic
is then called a statistic, and the probability distribution of the statistic  is defined by the formula
is defined by the formula
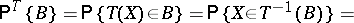 |
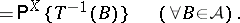 |
Examples.
1) Let  be independent identically-distributed random variables which have a variance. The statistics
be independent identically-distributed random variables which have a variance. The statistics
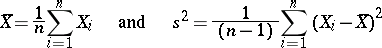 |
are then unbiased estimators for the mathematical expectation  and the variance
and the variance 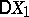 , respectively.
, respectively.
2) The terms of the variational series (series of order statistics, cf. Order statistic)
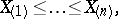 |
constructed from the observations  , are statistics.
, are statistics.
3) Let the random variables 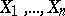 form a stationary stochastic process with spectral density
form a stationary stochastic process with spectral density 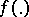 . In this case the statistic
. In this case the statistic
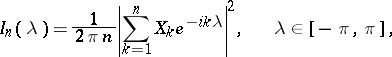 |
called the periodogram, is an asymptotically-unbiased estimator for 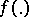 , given certain specific conditions of regularity on
, given certain specific conditions of regularity on  , i.e.
, i.e.
 |
In the theory of estimation and statistical hypotheses testing, great importance is attached to the concept of a sufficient statistic, which brings about a reduction of data without any loss of information on the (parametric) family of distributions under consideration.
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1988) |
| [2] | V.G. Voinov, M.S. Nikulin, "Unbiased estimates and their applications" , Moscow (1989) (In Russian) |
Statistics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistics&oldid=14854