Statistical mechanics, mathematical problems in
The totality of problems of mathematical physics that arise from trying to interpret accurately the basic concepts and facts of statistical mechanics. These problems can be conditionally divided into the following groups:
1) the foundations of the basic principles of statistical mechanics;
2) equilibrium ensembles at the thermodynamic limit, inference of thermodynamic relations;
3) phase transitions;
4) the evolution of ensembles, the relaxation problem, studies on kinetic and hydrodynamic equations;
5) basic states, elementary excitations (in the case of a quantum system).
In statistical mechanics, systems consisting of a large number of (microscopic) particles contained in a large (relative to the dimensions of the particles) domain 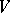 of the space
of the space 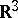 are studied. Statistical mechanics, depending on the method used to describe the system, is divided into classical and quantum mechanics.
are studied. Statistical mechanics, depending on the method used to describe the system, is divided into classical and quantum mechanics.
The description of the classical system contained in 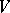 involves giving the space
involves giving the space 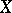 of possible states of each separate particle (single-particle space), as well as the totality
of possible states of each separate particle (single-particle space), as well as the totality  of admissible configurations
of admissible configurations 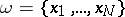 (
(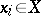 ,
, 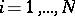 ,
, 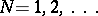 ) of a finite number of particles within
) of a finite number of particles within 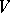 , and defining the energy
, and defining the energy  for every configuration
for every configuration 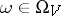 and the law of the evolution of the system in time (also called the dynamics), i.e. the semi-group (more often an entire group) of transformations
and the law of the evolution of the system in time (also called the dynamics), i.e. the semi-group (more often an entire group) of transformations 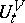 ,
, 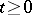 , of
, of 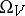 onto itself which preserve the energy
onto itself which preserve the energy 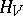 :
:
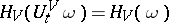 |
for any 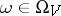 and any
and any 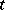 . In many cases,
. In many cases, 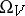 naturally has a symplectic structure, and the transformations
naturally has a symplectic structure, and the transformations 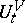 are produced by using solutions of the so-called Hamiltonian system of equations of motion, generated by the Hamilton function
are produced by using solutions of the so-called Hamiltonian system of equations of motion, generated by the Hamilton function 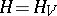 (see [1]). Moreover, a natural measure
(see [1]). Moreover, a natural measure 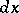 usually exists in the space
usually exists in the space 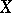 such that the measure
such that the measure 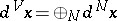 in
in 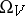 (
(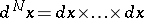 is the product measure on
is the product measure on 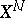 ) is invariant relative to the evolutions
) is invariant relative to the evolutions 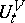 . However, for macroscopic systems consisting of a large number of particles, such a detailed description of their states and of the dynamics of these states (i.e. a description of the trajectories of each individual particle) proves to be almost impossible, and of no use anyway from the point of view of studying the macroscopic properties of the whole system. These properties are determined only by certain mean characteristics of the configuration
. However, for macroscopic systems consisting of a large number of particles, such a detailed description of their states and of the dynamics of these states (i.e. a description of the trajectories of each individual particle) proves to be almost impossible, and of no use anyway from the point of view of studying the macroscopic properties of the whole system. These properties are determined only by certain mean characteristics of the configuration  , and of its evolution
, and of its evolution 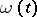 ,
, 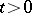 , in time: for example, the fractions
, in time: for example, the fractions 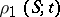 ,
, 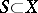 , of particles in
, of particles in 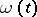 whose states belong to a given set
whose states belong to a given set  of a single-particle space
of a single-particle space 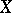 , or the fractions
, or the fractions 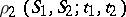 of particles whose states at the moment of time
of particles whose states at the moment of time 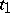 belong to the set
belong to the set 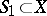 , and at the moment of time
, and at the moment of time 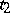 belong to the set
belong to the set 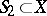 , etc.
, etc.
These concepts have given rise to the following radical idea: The state of a macroscopic system must be defined by a probability distribution 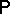 on the phase space
on the phase space  , whereby the evolution
, whereby the evolution 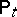 ,
,  , of this distribution in time is generated by the initial development of the system itself:
, of this distribution in time is generated by the initial development of the system itself:
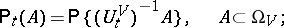 | (1) |
here 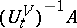 is the complete inverse image of the set
is the complete inverse image of the set 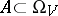 under the mapping
under the mapping 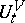 . This stipulation is complemented by the following postulate: For every "good" probability distribution
. This stipulation is complemented by the following postulate: For every "good" probability distribution 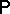 on the phase space
on the phase space 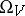 and an appropriate physical quantity
and an appropriate physical quantity 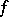 (i.e. a real-valued function on
(i.e. a real-valued function on 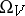 ), the values this quantity takes are, with probability close to one (calculated with respect to
), the values this quantity takes are, with probability close to one (calculated with respect to 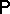 ), close to its mean value
), close to its mean value 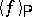 . One of the problems related to statistical mechanics is to put this assertion into an exact form. One of the possible results is of the following kind: Let the distribution
. One of the problems related to statistical mechanics is to put this assertion into an exact form. One of the possible results is of the following kind: Let the distribution 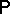 on
on 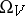 possess the property of rapidly-decreasing dependence (i.e. the probability distributions it generates of configurations for two subsystems, situated far apart, are almost independent), while the physical quantity is summable, i.e.
possess the property of rapidly-decreasing dependence (i.e. the probability distributions it generates of configurations for two subsystems, situated far apart, are almost independent), while the physical quantity is summable, i.e.
 | (2) |
where 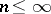 is arbitrary,
is arbitrary, 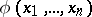 is a certain symmetric "local" function on
is a certain symmetric "local" function on 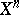 (i.e.
(i.e. 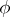 tends rapidly to zero as the points
tends rapidly to zero as the points  move further away from each other), and
move further away from each other), and 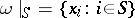 if
if 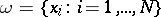 . In this case
. In this case 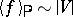 , and the fluctuation
, and the fluctuation 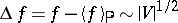 (with probability close to one for large
(with probability close to one for large 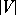 ), while the distribution of
), while the distribution of 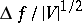 is close to normal (as before, when
is close to normal (as before, when 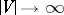 , see [2]).
, see [2]).
A probability distribution 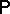 on a phase space is said to be an equilibrium distribution if it is invariant relative to the dynamics
on a phase space is said to be an equilibrium distribution if it is invariant relative to the dynamics 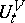 . Apart from the energy
. Apart from the energy 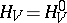 , let there be several more so-called integrals of motion
, let there be several more so-called integrals of motion 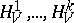 , i.e. functions on
, i.e. functions on  that are invariant relative to
that are invariant relative to 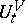 (for example, the number of particles in the system, the total momentum of the particles, the total spin, etc.). Every distribution on
(for example, the number of particles in the system, the total momentum of the particles, the total spin, etc.). Every distribution on 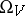 of the form
of the form
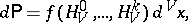 |
where 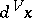 is the invariant measure on
is the invariant measure on 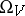 and
and 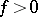 is a function (possibly generalized), is an equilibrium distribution. An equilibrium distribution defined by a density of the form
is a function (possibly generalized), is an equilibrium distribution. An equilibrium distribution defined by a density of the form
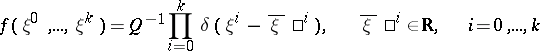 | (3) |
(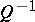 is a normalizing factor), is called a microcanonical distribution (or microcanonical ensemble), concentrated on the surface
is a normalizing factor), is called a microcanonical distribution (or microcanonical ensemble), concentrated on the surface
 | (4) |
of constancy of first integrals.
In statistical mechanics it is postulated that the microcanonical distribution (3) is an equilibrium distribution (i.e. the mean values of the physical variables calculated by means of (3) coincide with great accuracy with the experimentally-measured values). For a long time it was believed that in order to prove this postulate, an unknown ergodic hypothesis had to be demonstrated: If 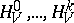 is a complete set of (smooth) integrals of motion, the microcanonical distribution is the unique (smooth) equilibrium distribution of any surface
is a complete set of (smooth) integrals of motion, the microcanonical distribution is the unique (smooth) equilibrium distribution of any surface 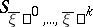 . Attempts to prove this hypothesis gave rise to modern ergodic theory (see [3], [4]). Now, however, it has become clear that the ergodicity of finite systems is an unnecessarily-strict assumption: In order to prove the postulate on microcanonical distributions it is sufficient to establish the ergodicity of the system at the thermodynamic limit
. Attempts to prove this hypothesis gave rise to modern ergodic theory (see [3], [4]). Now, however, it has become clear that the ergodicity of finite systems is an unnecessarily-strict assumption: In order to prove the postulate on microcanonical distributions it is sufficient to establish the ergodicity of the system at the thermodynamic limit  . Apart from the microcanonical distribution, the Gibbs equilibrium distribution (sometimes called a grand canonical ensemble) is often studied. It is defined by the density
. Apart from the microcanonical distribution, the Gibbs equilibrium distribution (sometimes called a grand canonical ensemble) is often studied. It is defined by the density
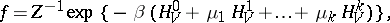 | (5) |
where 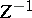 is a normalizing factor,
is a normalizing factor, 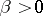 and
and 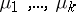 are arbitrary real parameters (the parameter
are arbitrary real parameters (the parameter  , where
, where 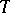 is the absolute temperature and
is the absolute temperature and 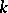 is an absolute constant, the so-called Boltzmann constant). Intermediate distributions are also sometimes studied (small canonical ensembles); these have a density of the form
is an absolute constant, the so-called Boltzmann constant). Intermediate distributions are also sometimes studied (small canonical ensembles); these have a density of the form
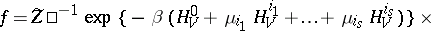 | (6) |
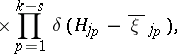 |
where 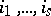 and
and 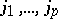 are two complementary subsets of indices in
are two complementary subsets of indices in 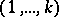 . The Gibbs distribution (5), as well as a distribution (6), is in many ways more convenient than the microcanonical distribution (3), and the use of both is justified by the following hypothesis — the so-called equivalence principle of ensembles: For "suitable" physical quantities on
. The Gibbs distribution (5), as well as a distribution (6), is in many ways more convenient than the microcanonical distribution (3), and the use of both is justified by the following hypothesis — the so-called equivalence principle of ensembles: For "suitable" physical quantities on 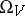 (for example, for a summable quantity of the form (2)), given values of the parameters
(for example, for a summable quantity of the form (2)), given values of the parameters 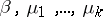 for which only one equilibrium phase exists, the mean
for which only one equilibrium phase exists, the mean 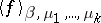 , calculated using the Gibbs distribution (5) for large
, calculated using the Gibbs distribution (5) for large 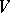 , is close to the mean
, is close to the mean 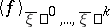 , calculated using a microcanonical ensemble on the surface
, calculated using a microcanonical ensemble on the surface 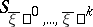 , where
, where 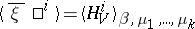 . The proof of this equivalence also constitutes one of the general mathematical problems of statistical mechanics and thermodynamics (see [5], [6], [7]).
. The proof of this equivalence also constitutes one of the general mathematical problems of statistical mechanics and thermodynamics (see [5], [6], [7]).
The accepted method of describing systems in statistical mechanics is justified when the domain 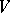 has sufficiently-large volume, in other words, statistical mechanics studies the asymptotic properties of systems in the limit
has sufficiently-large volume, in other words, statistical mechanics studies the asymptotic properties of systems in the limit 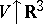 (i.e. a sequence of systems of one and the same particles, contained respectively in the volumes
(i.e. a sequence of systems of one and the same particles, contained respectively in the volumes  , where
, where 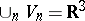 ). This passage to the limit is usually called a thermodynamic passage to the limit. One of the primary problems related to the thermodynamic limit is, beginning with equilibrium ensembles, to define the so-called thermodynamic potentials and relations. It proves possible to find all thermodynamic potentials, when
). This passage to the limit is usually called a thermodynamic passage to the limit. One of the primary problems related to the thermodynamic limit is, beginning with equilibrium ensembles, to define the so-called thermodynamic potentials and relations. It proves possible to find all thermodynamic potentials, when 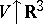 , from the asymptotics of the normalizing factors
, from the asymptotics of the normalizing factors 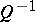 ,
, 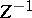 ,
,  , etc., in the ensembles (3), (5), (6); for example, the Gibbs thermodynamic potential is equal to
, etc., in the ensembles (3), (5), (6); for example, the Gibbs thermodynamic potential is equal to
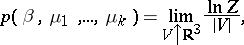 | (7) |
where 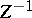 is the normalizing factor in the Gibbs ensemble (5). Other thermodynamic functions are introduced in the same way, and relations linking them are established. The majority of mathematical problems which arise here (existence of a limit, properties of thermodynamic potentials, etc.) have been studied fairly comprehensively, although a number of unsolved problems do remain (see, for example, [7]).
is the normalizing factor in the Gibbs ensemble (5). Other thermodynamic functions are introduced in the same way, and relations linking them are established. The majority of mathematical problems which arise here (existence of a limit, properties of thermodynamic potentials, etc.) have been studied fairly comprehensively, although a number of unsolved problems do remain (see, for example, [7]).
Since the end of the 1960's, the following general approach has found favour in mathematical statistical mechanics: instead of studying the asymptotic properties of finite systems in a thermodynamic passage to the limit, one should consider idealized infinite systems constructed in a particular way, whose characteristics coincide with the asymptotics being studied (this point of view was encountered in earlier works in less obvious form). Examining infinite systems gives a visible meaning to the somewhat formal procedure of a thermodynamic passage to the limit, and makes it possible to do without it altogether. The phase space 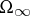 of an infinite system consists of infinite configurations of particles
of an infinite system consists of infinite configurations of particles 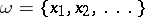 ,
, 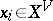 ,
, 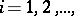 located throughout
located throughout 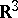 , while their dynamics
, while their dynamics 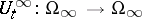 ,
, 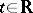 , is constructed as the limit of the dynamics
, is constructed as the limit of the dynamics 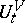 of finite systems as
of finite systems as 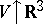 . The macroscopic states of an infinite system are defined by probability distributions on the space
. The macroscopic states of an infinite system are defined by probability distributions on the space 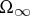 , which develop in line with the dynamics
, which develop in line with the dynamics 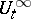 in
in 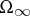 (see [1]). Limit Gibbs distributions
(see [1]). Limit Gibbs distributions 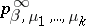 are introduced on
are introduced on 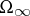 . They are constructed in a particular way by means of the Gibbs distributions (5)
. They are constructed in a particular way by means of the Gibbs distributions (5) 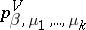 on finite systems (see [5], [9]). Although the introduction of infinite systems is a generally-accepted and fruitful method, it leads to complex intrinsic mathematical problems, which remain for the most part unsolved. These problems include, for example, the construction of a dynamics
on finite systems (see [5], [9]). Although the introduction of infinite systems is a generally-accepted and fruitful method, it leads to complex intrinsic mathematical problems, which remain for the most part unsolved. These problems include, for example, the construction of a dynamics 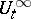 , the construction of limit Gibbs distributions, studies on their properties, etc.
, the construction of limit Gibbs distributions, studies on their properties, etc.
One of the main problems of statistical mechanics is the study of so-called phase transition, i.e. a sharp change of properties of a macroscopic system in a state of equilibrium, given a small change of the parameters describing this equilibrium — temperature, density of the particles, pressure, etc. In the modern mathematical approach, the problem of phase transition can be described in terms of limit Gibbs distributions in the following way: Given certain values of the parameters 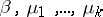 , it is possible, in general, to create a number of Gibbs distributions on
, it is possible, in general, to create a number of Gibbs distributions on 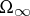 that are invariant relative to the action of the group
that are invariant relative to the action of the group 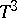 of shifts in
of shifts in 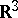 (or of a subgroup
(or of a subgroup 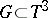 such that the quotient group
such that the quotient group 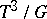 is compact), and are ergodic relative to this group (so-called pure phases). A point
is compact), and are ergodic relative to this group (so-called pure phases). A point 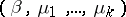 of the parameter space is said to be regular if it has a sufficiently small neighbourhood in which the structure of the set of pure phases, and their basic qualitative properties (for example, the character of decrease of the correlations), remains unaltered. It is assumed that all numerical characteristics of these distributions (correlation functions, semi-invariants, etc.) in a neighbourhood of regular points depend analytically on the parameters
of the parameter space is said to be regular if it has a sufficiently small neighbourhood in which the structure of the set of pure phases, and their basic qualitative properties (for example, the character of decrease of the correlations), remains unaltered. It is assumed that all numerical characteristics of these distributions (correlation functions, semi-invariants, etc.) in a neighbourhood of regular points depend analytically on the parameters 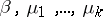 . All other (not regular) points in the parameter space are also points of phase transition. Thus, either a sharp change in the structure of the Gibbs distributions (say a new phase disappears or arises) or in their properties (for example, decrease of the correlations changes from exponential to gradual) takes place at such points of the phase space. Each of the characteristics of the distribution, as a function of
. All other (not regular) points in the parameter space are also points of phase transition. Thus, either a sharp change in the structure of the Gibbs distributions (say a new phase disappears or arises) or in their properties (for example, decrease of the correlations changes from exponential to gradual) takes place at such points of the phase space. Each of the characteristics of the distribution, as a function of 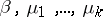 , is considered to have a singularity at a point of phase transition. Describing the structure of phases and their properties for every concrete system, defining points of phase transition and the character of the singularities at these points, as well as other tasks, also constitute the problem of phase transition. Although a large class of model systems exists for which (at low temperatures) a number of general methods of solving this problem have been worked out (see [9]), the theory of phase transition is still far from being perfect. The study of the so-called critical points is particularly complex (roughly speaking, the fusion of various phases takes place at these points; see [10]), in that, at these points, the decrease of the correlations of the Gibbs distribution is very slow.
, is considered to have a singularity at a point of phase transition. Describing the structure of phases and their properties for every concrete system, defining points of phase transition and the character of the singularities at these points, as well as other tasks, also constitute the problem of phase transition. Although a large class of model systems exists for which (at low temperatures) a number of general methods of solving this problem have been worked out (see [9]), the theory of phase transition is still far from being perfect. The study of the so-called critical points is particularly complex (roughly speaking, the fusion of various phases takes place at these points; see [10]), in that, at these points, the decrease of the correlations of the Gibbs distribution is very slow.
Many problems of statistical mechanics are related to the study of the time-development of distributions on a phase space, and particularly to the problem of relaxation, i.e. of approach to equilibrium. It is thought that, over a long period of time, every distribution on a phase space is approximated by an equilibrium (Gibbs) distribution. Despite the fact that many general representations of the mechanism of this process have been worked out, and that a number of simplified models have been studied, no complete theory exists yet (1991). The basic representations of the relaxation process (for the most part, they are still hypothetical) reduce to the fact that this process has three stages. At the first stage (while collisions of several particles are taking place), the distribution 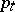 leads to a development of the system which is completely defined by a change of the first correlation function (i.e. by a distribution in a single-particle space
leads to a development of the system which is completely defined by a change of the first correlation function (i.e. by a distribution in a single-particle space 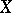 ). At the second stage — the kinetic stage, which lasts throughout the "free path" of the particle — the change of the first correlation function crosses over to a development in which everything depends only on the mean values of the particles, their speed, density, energy, etc. Lastly, there is the hydrodynamic stage, during which (as with macroscopic time) these mean values of density, speed, etc., are approximated by equilibrium values (see [11], [12]). Proving this scenario as a whole or in its separate parts is a complex mathematical problem, which is far from being completely solved (1991). Various systems of kinetic equations constitute a fundamental method of research. They are both exact, i.e. resulting directly from the definition of the Liouville equation (the hierarchical BBGKY chain — Bogolyubov, Born, Green, Kirkwood, Yvon) and approximate (the equations of Boltzmann, Chapman–Enskog, Vlasov–Landau, the hydrodynamic equations, etc.). These equations and their relation with the true picture of the evolution are also the subject of intensive mathematical study (cf. Bogolyubov chain of equations; Boltzmann equation; Chapman–Enskog method; Vlasov kinetic equation).
). At the second stage — the kinetic stage, which lasts throughout the "free path" of the particle — the change of the first correlation function crosses over to a development in which everything depends only on the mean values of the particles, their speed, density, energy, etc. Lastly, there is the hydrodynamic stage, during which (as with macroscopic time) these mean values of density, speed, etc., are approximated by equilibrium values (see [11], [12]). Proving this scenario as a whole or in its separate parts is a complex mathematical problem, which is far from being completely solved (1991). Various systems of kinetic equations constitute a fundamental method of research. They are both exact, i.e. resulting directly from the definition of the Liouville equation (the hierarchical BBGKY chain — Bogolyubov, Born, Green, Kirkwood, Yvon) and approximate (the equations of Boltzmann, Chapman–Enskog, Vlasov–Landau, the hydrodynamic equations, etc.). These equations and their relation with the true picture of the evolution are also the subject of intensive mathematical study (cf. Bogolyubov chain of equations; Boltzmann equation; Chapman–Enskog method; Vlasov kinetic equation).
Quantum statistical mechanics is based on the same principles as classical mechanics. The quantum description of a system of particles located within a domain 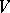 requires that a Hilbert space
requires that a Hilbert space 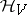 be given (the state space of the system), and that a self-adjoint operator
be given (the state space of the system), and that a self-adjoint operator 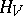 , operating on
, operating on 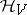 , be given (the energy operator of the system). The dynamics of the system is defined by the group
, be given (the energy operator of the system). The dynamics of the system is defined by the group 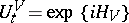 ,
, 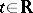 , of unitary operators operating on
, of unitary operators operating on 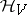 , whereby the dynamics
, whereby the dynamics 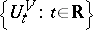 generates a group of automorphisms
generates a group of automorphisms 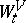 of the algebra
of the algebra 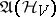 of bounded operators (observables) on
of bounded operators (observables) on 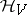 :
:
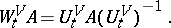 |
The change to the statistical description in the quantum case plays a role in defining a certain "mean" 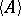 on the algebra
on the algebra 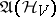 , i.e. of a positive linear functional
, i.e. of a positive linear functional 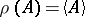 on this algebra, usually called a state. Every state on
on this algebra, usually called a state. Every state on 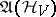 can be written in the form
can be written in the form
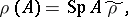 |
where 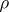 is a positive nuclear operator from
is a positive nuclear operator from 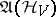 and
and 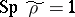 . The operator
. The operator 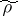 is usually called the density matrix of the state
is usually called the density matrix of the state 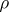 . The evolution in time of the state
. The evolution in time of the state 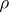 is defined by the evolution
is defined by the evolution 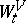 of the algebra itself:
of the algebra itself: 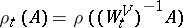 . States that are invariant relative to this evolution are called equilibrium states, as before. For a system in which, apart from the energy
. States that are invariant relative to this evolution are called equilibrium states, as before. For a system in which, apart from the energy 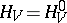 , there are several pairwise-commuting integrals of motion
, there are several pairwise-commuting integrals of motion 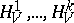 , the equilibrium state with density matrix
, the equilibrium state with density matrix
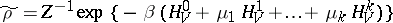 |
is called a Gibbs state (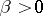 and
and 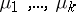 are parameters,
are parameters, 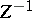 is a normalizing factor). An infinite quantum system is introduced in the same way as for a classical system by passage to the thermodynamic limit
is a normalizing factor). An infinite quantum system is introduced in the same way as for a classical system by passage to the thermodynamic limit 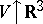 (see [5]). In order to describe this system, the
(see [5]). In order to describe this system, the 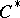 -algebra
-algebra 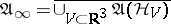 is examined (the bar signifies closure in the uniform topology), which is called the algebra of quasi-local observables, while the evolution
is examined (the bar signifies closure in the uniform topology), which is called the algebra of quasi-local observables, while the evolution 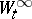 in
in 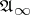 is defined as the limit of the evolutions
is defined as the limit of the evolutions 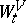 on the finite algebras
on the finite algebras 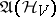 . It is possible to introduce limit Gibbs states on the algebra
. It is possible to introduce limit Gibbs states on the algebra 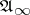 in the same way as for classical systems (see [5]). The problem of phase transitions in quantum systems is formulated in the same way as for classical systems in terms of limit Gibbs states.
in the same way as for classical systems (see [5]). The problem of phase transitions in quantum systems is formulated in the same way as for classical systems in terms of limit Gibbs states.
Finally, in quantum statistical mechanics there also exists a whole circle of kinetic problems; however, the mechanism of relaxation processes in quantum mechanics is more complicated than in classical mechanics, and is less studied.
There exist specific results on the so-called groundstate of a system in the quantum case (corresponding to zero temperature) and on perturbations of this state of finite energy. A number of interesting problems is related to this problem (superconductivity, superfluidity), emerging at low temperatures [13]. Problems on the construction and study of quantum fields may be investigated by means of the theory of Gibbs fields, as developed in statistical mechanics (see [14], [15]).
References
| [1] | V.I. Arnol'd, "Mathematical methods of classical mechanics" , Springer (1978) (Translated from Russian) |
| [2] | B.S. Nakhapetyan, "The central limit theorem for random fields with mixing property" R.L. Dobrushin (ed.) Ya.G. Sinai (ed.) , Multi-component random systems , M. Dekker (1980) pp. 531–547 (Translated from Russian) |
| [3] | I.P. [I.P. Kornfel'd] Cornfel'd, S.V. Fomin, Ya.G. Sinai, "Ergodic theory" , Springer (1982) (Translated from Russian) |
| [4] | N.S. Krylov, "Works on the foundation of statistical physics" , Princeton Univ. Press (1979) (Translated from Russian) |
| [5] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1966) |
| [6] | A.M. [A.M. Khalfina] Halfina, "The limiting equivalence of the canonical and grand canonical ensembles (low density case)" Math. USSR Sb. , 9 : 1 (1969) pp. 1–52 Mat. Sb. , 80 (1969) pp. 3–51 |
| [7] | R.A. Minlos, A. Khaitov, "Limiting equivalence of thermodynamic ensembles in the case of one-dimensional systems" Trans. Moscow Math. Soc. , 32 (1975) pp. 143–180 Tr. Moskov. Mat. Obshch. , 32 (1975) pp. 147–186 |
| [8] | O.E. Lanford, , Gibbs states in statistical physics , Moscow (1978) pp. 159–218 (In Russian; translated from English) |
| [9] | Ya.G. Sinai, "Theory of phase transitions: rigorous results" , Pergamon (1982) (Translated from Russian) |
| [10] | H.E. Stanley, "Phase transitions and critical phenomena" , Clarendon Press (1971) |
| [11] | R. Libov, "Introduction to the theory of kinetic equations" , Wiley (1969) |
| [12] | R. Balescu, "Equilibrium and non-equilibrium statistical mechanics" , 1–2 , Wiley (1975) |
| [13] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1980) (Translated from Russian) |
| [14] | B. Simon, "The  Euclidean (quantum) field theory" , Princeton Univ. Press (1974) Euclidean (quantum) field theory" , Princeton Univ. Press (1974) |
| [15] | , Euclidean quantum field theory. The Markov approach , Moscow (1978) (In Russian; translated from English) |
| [16] | J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981) |
| [17] | V.A. Malyshev, R.A. Minlos, "Gibbs random fields" , Kluwer (1991) (Translated from Russian) |
Comments
References
| [a1] | C. Cercignani, "The Boltzmann equation and its applications" , Springer (1988) |
| [a2] | C. Cercignani, "Mathematical methods in kinetic theory" , Plenum (1990) |
| [a3] | R.L. Dobrushin (ed.) , Mathematical problems of statistical mechanics and dynamics. A collection of surveys , Reidel (1986) |
Statistical mechanics, mathematical problems in. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_mechanics,_mathematical_problems_in&oldid=18154