Statistical ensemble
A name given in statistical physics (cf. Statistical physics, mathematical problems in) to the phase space (space of states) of any physical system and a method of averaging physical (observable) quantities related to this system. In a classical system with phase space  , the observable quantities are real functions defined on
, the observable quantities are real functions defined on  , and they are averaged by integration with respect to a certain probability measure
, and they are averaged by integration with respect to a certain probability measure 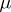 on
on  . In a quantum system described by vectors in a Hilbert space
. In a quantum system described by vectors in a Hilbert space 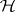 , the observable quantities are defined by self-adjoint operators acting on
, the observable quantities are defined by self-adjoint operators acting on 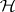 , and are averaged using a certain positive, normalized functional
, and are averaged using a certain positive, normalized functional 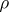 , defined on the algebra
, defined on the algebra 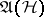 of operators on
of operators on 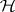 (such functionals on
(such functionals on 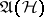 are called states). A state is usually given in the form
are called states). A state is usually given in the form
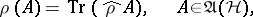 | (1) |
where 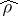 is a positive operator on
is a positive operator on 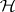 (of trace class) such that
(of trace class) such that 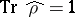 (the operator
(the operator 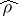 is called the density matrix of the state
is called the density matrix of the state 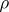 ).
).
If the evolution of the physical system in time is given (the dynamics of the system), i.e. (in the classical case) a group 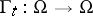 ,
, 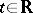 , of one-to-one mappings of the phase space onto itself, generated by the Hamilton equations of motion with a certain Hamilton function
, of one-to-one mappings of the phase space onto itself, generated by the Hamilton equations of motion with a certain Hamilton function 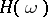 ,
, 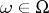 (the energy of the system), or (in the quantum case) a group of unitary mappings
(the energy of the system), or (in the quantum case) a group of unitary mappings 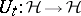 ,
, 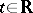 , of the Hilbert space onto itself, generated by the Hamilton operator
, of the Hilbert space onto itself, generated by the Hamilton operator 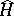 (the energy operator of the system), then the evolution in time of any statistical ensemble defined for this system is naturally defined:
(the energy operator of the system), then the evolution in time of any statistical ensemble defined for this system is naturally defined:
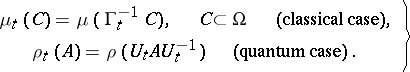 | (2) |
In describing the stationary behaviour of the system, equilibrium ensembles are studied, i.e. measures or states that are invariant relative to the evolution (2). Although there are, generally speaking, many equilibrium statistical ensembles, only special ones are studied in statistical physics — the so-called canonical Gibbs ensembles (distributions) (cf. also Gibbs statistical aggregate).
Classical Gibbs ensembles.
In addition to the Hamiltonian 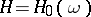 , let there be a functionally independent set
, let there be a functionally independent set 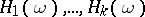 ,
, 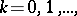 of functions on
of functions on  that are invariant relative to the dynamics
that are invariant relative to the dynamics 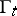 (in systems consisting of a finite, but arbitrary, number of particles of one or more types,
(in systems consisting of a finite, but arbitrary, number of particles of one or more types, 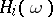 is equal, for example, to the number of particles of whatever type in the configuration
is equal, for example, to the number of particles of whatever type in the configuration 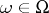 ; in the case of a system of magnetic dipoles,
; in the case of a system of magnetic dipoles, 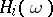 is equal to their total magnetic moment, etc.). The measure
is equal to their total magnetic moment, etc.). The measure
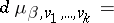 | (3) |
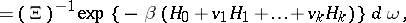 |
is called a grand canonical Gibbs ensemble, where 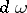 is a measure generated by a symplectic structure on
is a measure generated by a symplectic structure on  ;
; 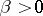 and
and  are real parameters; and
are real parameters; and 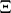 is a normalization factor, called the grand statistical sum (or grand partition function, cf. Statistical sum),
is a normalization factor, called the grand statistical sum (or grand partition function, cf. Statistical sum),
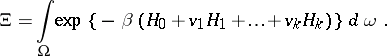 | (4) |
The measure 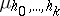 generated by the measure (3), concentrated on the set
generated by the measure (3), concentrated on the set 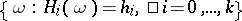 ,
, 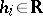 ,
,  , and coinciding with the conditional distribution on this set is called a micro-canonical Gibbs ensemble. "Intermediate" ensembles are also studied — the so-called small canonical Gibbs ensembles, which are obtained in similar fashion from (3) by fixing the values of all or some of the functions
, and coinciding with the conditional distribution on this set is called a micro-canonical Gibbs ensemble. "Intermediate" ensembles are also studied — the so-called small canonical Gibbs ensembles, which are obtained in similar fashion from (3) by fixing the values of all or some of the functions 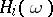 ,
, 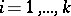 .
.
Quantum Gibbs ensembles.
Let 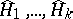 (
(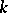 arbitrary) be pairwise commuting operators, commuting also with the operator
arbitrary) be pairwise commuting operators, commuting also with the operator 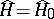 ( "conserved quantities" ). The state on
( "conserved quantities" ). The state on 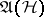 defined by the density matrix
defined by the density matrix
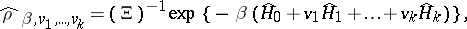 |
where
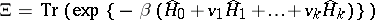 |
is a grand statistical sum (grand partition function) and 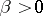 ,
,  are parameters, is called the grand canonical Gibbs ensemble. Let
are parameters, is called the grand canonical Gibbs ensemble. Let 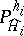 ,
, 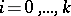 , be a projector on
, be a projector on 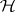 onto the eigensubspace of the operator
onto the eigensubspace of the operator 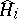 with eigenvalue
with eigenvalue 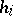 . A state with density matrix
. A state with density matrix
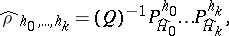 |
where 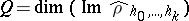 , is called a micro-canonical Gibbs ensemble. Small canonical Gibbs ensembles are introduced in the same way, for example, as a statistical ensemble with density matrix
, is called a micro-canonical Gibbs ensemble. Small canonical Gibbs ensembles are introduced in the same way, for example, as a statistical ensemble with density matrix
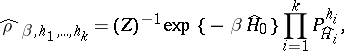 |
where 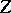 is a normalization factor (a small statistical sum, small partition function).
is a normalization factor (a small statistical sum, small partition function).
Certain model modifications of these statistical ensembles are sometimes studied (for example, Gibbs ensembles in configuration or lattice systems), as are so-called limiting Gibbs ensembles, i.e. probability distributions (or states) on the phase space of an infinite system (for example, systems with an infinite number of particles moving throughout the space). These statistical ensembles arise from the above ensembles for finite systems during a passage to the thermodynamic limit (see [3]).
There exists a hypothesis — the so-called principle of limit equivalence of ensembles — which states that when certain natural conditions are fulfilled (roughly speaking, when there is no phase transition), limiting Gibbs statistical ensembles obtained using different Gibbs ensembles (grand canonical, small canonical, micro-canonical) coincide, given a specific correspondence between the parameters defining these ensembles. This hypothesis has been proved (see [3]) in certain specific situations.
References
| [1] | L.D. Landau, E.M. Lifshitz, "Statistical physics" , Pergamon (1980) (Translated from Russian) |
| [2] | R.A. Minlos, "Lectures on statistical physics" Russian Math. Surveys , 23 : 1 (1968) pp. 137–201 Uspekhi Mat. Nauk , 23 : 1 (1968) pp. 133–190 |
| [3] | D. Ruelle, "Statistical mechanics: rigorous results" , Benjamin (1969) |
| [4] | K. Preston, "Gibbs states and countable sets" , Cambridge Univ. Press (1974) |
Statistical ensemble. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Statistical_ensemble&oldid=11445