Stationary distribution

A probability distribution for a homogeneous Markov chain that is independent of time. Let 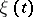be a homogeneous Markov chain with set of states and transition probabilities . A stationary distribution is a set of numbers such that

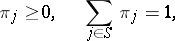(1)

(2)

The equalities (2) signify that a stationary distribution is invariant in time: If , , then for any 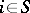, 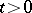; moreover, for any , ,

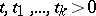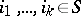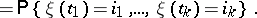If 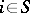is a state of the Markov chain 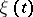for which the limits

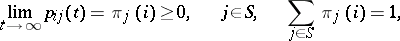exist, then the set of numbers 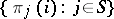satisfies (2) and is a stationary distribution of the chain 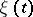(see also Transition probabilities).

The system of linear equations (2) relative to 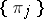, given the supplementary conditions (1), has a unique solution if the number of classes of positive states of the Markov chain 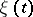is equal to 1; if the chain has 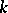classes of positive states, then the set of its stationary distributions is the convex hull of stationary distributions, each of which is concentrated on one class (see Markov chain, class of positive states of a).

Any non-negative solution of the system (2) is called a stationary measure; a stationary measure can exist also when (1) and (2) are not compatible. For example, a random walk on :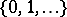

where 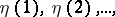are independent random variables such that

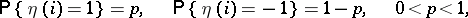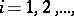does not have a stationary distribution, but has a stationary measure:

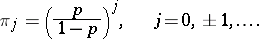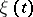One of the possible probabilistic interpretations of a stationary measure of a Markov chain with set of states 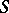is as follows. Let there be a countable set of independent realizations of 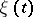, and let 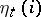be the number of realizations for which 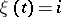. If the random variables 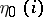, , 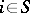are independent and are subject to Poisson distributions with respective means , , 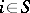then for any 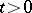the random variables , , 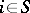are independent and have the same distributions as , .

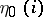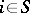References

[1]	K.L. Chung, "Markov chains with stationary transition probabilities" , Springer (1960)
[2]	S. Karlin, "A first course in stochastic processes" , Acad. Press (1966)

Comments

Stationary distributions are also defined for more general Markov processes, see e.g. [a1].

References

[a1]	L.P. Breiman, "Probability" , Addison-Wesley (1968)