Star-like domain

with respect to a fixed point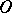

A domain 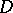in the complex space 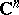, , 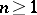such that, for any point of 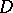, the segment of the straight line from that point to 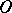lies entirely in .

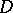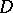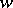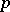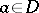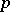A simply-connected open Riemann surface over the -plane is called a -sheeted star-like domain with respect to a fixed point (where is a natural number) if there exist points of 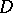above (counting multiplicities) and if, for any point 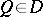, there is a path 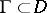from 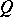to one of the points above such that the projection of 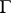on the -plane is the straight-line segment joining the projection of 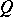to .

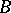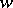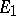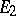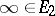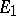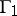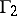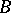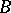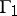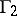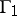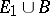Let be a doubly-connected domain in the -plane, let and be complementary continua, , let be a fixed point of , and let and be the boundary components of . Then is said to be star-like with respect to if either each of the simply-connected domains containing and bounded by and is star-like, or is the union of the straight-line segments issuing from and is star-like with respect to .

References

[1]	G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian)
[2]	J.A. Hummel, "Multivalent starlike functions" J. d'Anal. Math. , 18 (1967) pp. 133–160

Comments

For 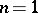, star-like domains are the images of the unit disc under star-like functions (cf. Star-like function).