Stable rank
Let 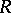 be an associative ring with unit element. A sequence of elements
be an associative ring with unit element. A sequence of elements 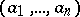 is called left unimodular if the left ideal generated by the
is called left unimodular if the left ideal generated by the 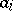 ,
, 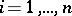 , is all of
, is all of 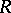 .
.
The left stable rank of 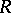 is the least integer
is the least integer  such that for each
such that for each 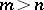 and left unimodular sequence
and left unimodular sequence 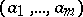 there are
there are 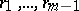 such that
such that 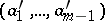 with
with 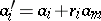 ,
, 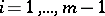 , is also left unimodular.
, is also left unimodular.
The right stable rank of 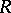 is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [a1], cf. also, e.g., [a2], §11.3, and both are therefore called the stable rank of
is defined analogously by replacing left with right everywhere. The left and right stable ranks are equal [a1], cf. also, e.g., [a2], §11.3, and both are therefore called the stable rank of 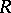 , denoted by
, denoted by 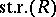 .
.
By writing a left unimodular sequence 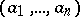 as a column, there is a natural left action of
as a column, there is a natural left action of  on
on 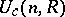 , the set of all left unimodular sequences of length
, the set of all left unimodular sequences of length  . The general linear rank,
. The general linear rank, 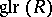 , of
, of 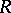 is the least integer
is the least integer  such that
such that 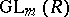 acts transitively on
acts transitively on  for all
for all 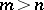 . This is equivalent to the property that all right stably-free modules of rank
. This is equivalent to the property that all right stably-free modules of rank 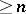 are free, [a2].
are free, [a2].
Recall that 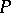 is stably free if
is stably free if 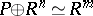 for some
for some 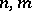 ; the rank of
; the rank of 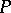 is then defined as
is then defined as 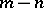 . This is well-defined if
. This is well-defined if 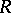 has the invariant basis property (i.e.
has the invariant basis property (i.e. 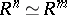 if and only if
if and only if 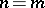 ). This property holds, e.g., if
). This property holds, e.g., if 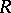 is commutative or right Noetherian.
is commutative or right Noetherian.
One has 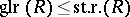 , so that any stably-free module of rank
, so that any stably-free module of rank 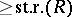 is free.
is free.
For a field 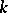 one has
one has 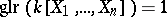 for all
for all  .
.
Let 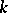 be a field of transcendence degree
be a field of transcendence degree 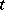 over its prime subfield
over its prime subfield 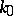 . The Kronecker dimension of
. The Kronecker dimension of 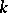 is then defined as
is then defined as 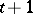 if
if 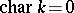 and as
and as 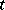 otherwise. For
otherwise. For 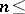 Kronecker dimension of
Kronecker dimension of 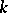 ,
, 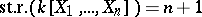 . If
. If 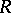 is commutative of Krull dimension
is commutative of Krull dimension  (cf. also Dimension of an associative ring), then
(cf. also Dimension of an associative ring), then 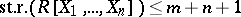 (Bass' theorem).
(Bass' theorem).
Let 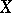 be a topological space,
be a topological space, 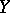 a metric space and
a metric space and 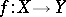 a continuous mapping. A point
a continuous mapping. A point 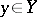 is a stable value of
is a stable value of  if it is in
if it is in 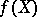 and if there is an
and if there is an  such that for every continuous mapping
such that for every continuous mapping 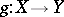 with
with 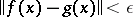 for all
for all 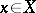 it is still true that
it is still true that 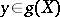 . The mapping dimension of a topological space
. The mapping dimension of a topological space 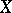 ,
, 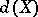 , is the largest integer
, is the largest integer 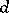 for which there exists a mapping
for which there exists a mapping 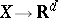 for which the origin is a stable value. (If no such
for which the origin is a stable value. (If no such 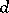 exists,
exists, 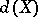 is set equal to
is set equal to 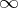 .) For nice spaces, e.g., metrizable, separable,
.) For nice spaces, e.g., metrizable, separable,  , this concept of dimension coincides with other notions of dimension, such as inductive dimension, [a5], Chapt. VI, §1 (cf. Dimension theory). It always coincides with the notion of dimension defined by essential mappings (cf. Dimension theory), [a5], Chapt. VI, §3.
, this concept of dimension coincides with other notions of dimension, such as inductive dimension, [a5], Chapt. VI, §1 (cf. Dimension theory). It always coincides with the notion of dimension defined by essential mappings (cf. Dimension theory), [a5], Chapt. VI, §3.
Let 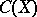 be the ring of real-valued continuous functions on a topological space
be the ring of real-valued continuous functions on a topological space  and
and 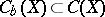 the subring of bounded functions. Then
the subring of bounded functions. Then 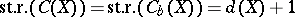 (Vaserstein's theorem).
(Vaserstein's theorem).
Both Bass' and Vaserstein's theorem indicate that 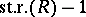 is a good dimension concept for rings.
is a good dimension concept for rings.
More generally, the stable rank is defined for subrings and ideals of an associative ring 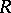 with unit.
with unit.
Let 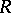 be an associative ring with unit, and let
be an associative ring with unit, and let 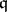 be a subring (possibly without unit) of
be a subring (possibly without unit) of 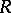 . A sequence of elements
. A sequence of elements 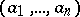 is left
is left 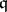 -unimodular if it is left unimodular (in
-unimodular if it is left unimodular (in 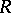 ) and, moreover,
) and, moreover, 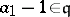 ,
, 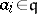 ,
, 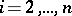 . The stable rank of the subring
. The stable rank of the subring 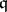 is the least number
is the least number  such that for each left
such that for each left 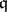 -unimodular sequence
-unimodular sequence  of length
of length 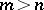 there are
there are 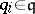 ,
, 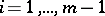 , such that
, such that 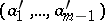 , with
, with 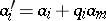 , is a left
, is a left 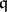 -unimodular sequence of length
-unimodular sequence of length 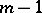 . (Such a property is referred to as a stable range condition, cf., e.g., [a4]). The stable rank of
. (Such a property is referred to as a stable range condition, cf., e.g., [a4]). The stable rank of 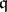 does not depend on the ambient ring
does not depend on the ambient ring 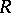 . Again it is true that the notion of stable rank is left/right symmetric, [a1].
. Again it is true that the notion of stable rank is left/right symmetric, [a1].
References
| [a1] | L.N. Vaserstein, "Stable ranks of rings and dimensionality of topological spaces" Funct. Anal. Appl. , 5 (1971) pp. 102–110 Funkts. Anal. i Prilozhen. , 5 : 2 (1970) pp. 17–27 |
| [a2] | J.C. McConnell, J.C. Robson, "Noncommutative Noetherian rings" , Wiley (1987) |
| [a3] | A.J. Hahn, O.T. O'Meara, "The classical groups and 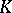 -theory" , Springer (1981) pp. §4.1 -theory" , Springer (1981) pp. §4.1 |
| [a4] | H. Bass, "Algebraic 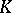 -theory" , Benjamin (1968) pp. Chapt. V, §3 -theory" , Benjamin (1968) pp. Chapt. V, §3 |
| [a5] | W. Hurevicz, G. Wallman, "Dimension theory" , Princeton Univ. Press (1948) |
Stable rank. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stable_rank&oldid=12780