Stable and unstable theories
A branch of model theory dealing with the stability of elementary theories (cf. Elementary theory). Let 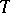 be a complete theory of the first order, of signature (language)
be a complete theory of the first order, of signature (language)  , let
, let 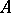 be a model of
be a model of 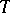 and let
and let 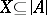 . The signature
. The signature 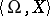 is obtained from
is obtained from  by adding isolated element symbols
by adding isolated element symbols 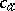 for all
for all 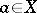 . The system
. The system 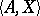 has signature
has signature  and is an enrichment (simple expansion) of the model
and is an enrichment (simple expansion) of the model 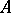 , in which
, in which 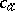 is interpreted as
is interpreted as  for all
for all 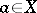 . The theory
. The theory 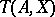 is the totality of formulas of signature
is the totality of formulas of signature 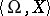 that are true in
that are true in 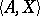 . A set
. A set  of formulas
of formulas 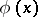 in the language
in the language 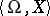 with one free variable
with one free variable  is a type of
is a type of 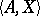 if
if  is satisfiable.
is satisfiable.  is the collection of all maximal types of
is the collection of all maximal types of 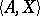 . The theory
. The theory 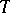 is said to be stable at cardinality
is said to be stable at cardinality 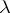 if for any model
if for any model 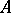 of
of 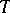 and any
and any 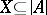 of cardinality not exceeding
of cardinality not exceeding 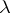 , the cardinality of
, the cardinality of  also does not exceed
also does not exceed 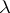 . A theory is called stable if it is stable at even one infinite cardinality.
. A theory is called stable if it is stable at even one infinite cardinality.
Let 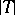 denote the cardinality of the set of formulas of signature
denote the cardinality of the set of formulas of signature  . If
. If 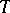 is stable, then it is stable at all cardinalities that satisfy the equality
is stable, then it is stable at all cardinalities that satisfy the equality 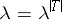 . If
. If 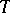 is stable, then there exist a model
is stable, then there exist a model 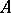 of
of 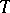 and an infinite set
and an infinite set 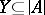 such that for any formula
such that for any formula 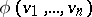 of signature
of signature  and for any two sequences
and for any two sequences 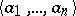 ,
, 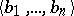 of different elements of
of different elements of 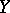 , the truth of
, the truth of 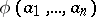 in
in 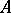 is equivalent to the truth of
is equivalent to the truth of 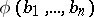 in
in 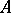 ; the set
; the set 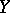 is then called the set of indistinguishable elements in
is then called the set of indistinguishable elements in 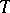 . A characteristic property of unstable theories is the existence of a set which has somehow opposite properties. Namely, the instability of a theory
. A characteristic property of unstable theories is the existence of a set which has somehow opposite properties. Namely, the instability of a theory 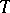 is equivalent to the existence of a formula
is equivalent to the existence of a formula 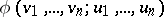 of signature
of signature  , of a model
, of a model 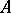 of
of 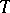 and of a sequence
and of a sequence 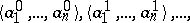 of tuples of elements of
of tuples of elements of 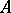 , such that the truth of
, such that the truth of 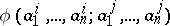 in
in 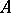 is equivalent to the inequality
is equivalent to the inequality 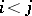 . For this reason, complete extensions of the theory of totally ordered sets with infinite models, as well as the theory of any infinite Boolean algebra, are unstable. In particular, the theory of natural numbers with addition and the theory of the field of real numbers are unstable. If a theory
. For this reason, complete extensions of the theory of totally ordered sets with infinite models, as well as the theory of any infinite Boolean algebra, are unstable. In particular, the theory of natural numbers with addition and the theory of the field of real numbers are unstable. If a theory 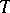 is unstable, then the number of isomorphism types of models of
is unstable, then the number of isomorphism types of models of 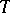 at every uncountable cardinal number
at every uncountable cardinal number 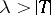 is equal to
is equal to 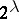 . A theory
. A theory 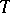 that is categorical at an uncountable cardinal number
that is categorical at an uncountable cardinal number 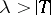 (cf. Categoricity in cardinality) is therefore stable. There do exist stable theories, however, that are not categorical at any infinite cardinality. Such an example is the theory
(cf. Categoricity in cardinality) is therefore stable. There do exist stable theories, however, that are not categorical at any infinite cardinality. Such an example is the theory 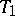 whose signature consists of a one-place predicate and a countable set of isolated elements. The axioms of this theory state that a predicate is true on the isolated elements, divides every model of
whose signature consists of a one-place predicate and a countable set of isolated elements. The axioms of this theory state that a predicate is true on the isolated elements, divides every model of  into two infinite sets, and that the isolated elements are not equal to each other.
into two infinite sets, and that the isolated elements are not equal to each other.
Theories of finite or countable signature that are stable at a countable cardinality are also said to be totally transcendental. Every totally transcendental theory is stable at all infinite cardinalities. Every categorical theory of finite or countable signature at an uncountable cardinality is totally transcendental. The theory 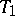 above is totally transcendental. Totally transcendental theories can also be characterized in other terms. Let
above is totally transcendental. Totally transcendental theories can also be characterized in other terms. Let  be a complete theory of finite or countable signature
be a complete theory of finite or countable signature  and let
and let 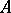 be an infinite model of
be an infinite model of 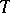 . A formula
. A formula 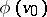 of signature
of signature 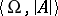 is given the rank
is given the rank 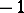 if it is false on all elements of the model
if it is false on all elements of the model 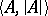 , and the rank
, and the rank 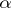 (
(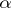 is an ordinal number) if it does not have any rank lower than
is an ordinal number) if it does not have any rank lower than  ; however, for every elementary extension
; however, for every elementary extension 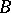 of the system
of the system 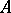 , and for every formula
, and for every formula 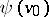 of signature
of signature 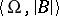 , one of the formulas
, one of the formulas 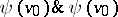 or
or 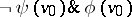 is given a rank less than
is given a rank less than 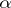 . A theory
. A theory 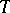 is totally transcendental if and only if for every model
is totally transcendental if and only if for every model  of
of 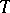 , each formula
, each formula  of signature
of signature 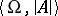 is given a certain rank.
is given a certain rank.
References
| [1] | S. Shelah, "Stability, the f.c.p., and superstability; model theoretic properties of formulas in first order theory" Ann. of Math. Logic , 3 : 3 (1971) pp. 271–362 |
| [2] | S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1990) |
Comments
See also Stability theory (in logic).
References
| [a1] | J.T. Baldwin, "Fundamentals of stability theory" , Springer (1988) |
| [a2] | D. Lascar, "Stability in model theory" , Wiley (1987) |
| [a3] | A. Pillay, "An introduction to stability theory" , Clarendon Press (1983) |
| [a4] | C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1990) |
Stable and unstable theories. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stable_and_unstable_theories&oldid=16041