Stabilizer
of an element  in a set
in a set 
The subgroup  of a group of transformations
of a group of transformations  , operating on a set
, operating on a set  , consisting of the transformations that leave the element
, consisting of the transformations that leave the element  fixed:
fixed:  . The stabilizer of
. The stabilizer of  is also called the isotropy group of
is also called the isotropy group of  , the isotropy subgroup of
, the isotropy subgroup of  or the stationary subgroup of
or the stationary subgroup of  . If
. If  ,
, 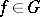 and
and  , then
, then 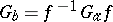 . If one considers the action of the group
. If one considers the action of the group 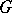 on itself by conjugation, the stabilizer of the element
on itself by conjugation, the stabilizer of the element  will be the centralizer of this element in
will be the centralizer of this element in  ; if the group acts by conjugation on the set of its subgroups, then the stabilizer of a subgroup
; if the group acts by conjugation on the set of its subgroups, then the stabilizer of a subgroup 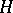 will be the normalizer of this subgroup (cf. Normalizer of a subset).
will be the normalizer of this subgroup (cf. Normalizer of a subset).
Comments
In case 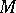 is a set of mathematical structures, for instance a set of lattices in
is a set of mathematical structures, for instance a set of lattices in  , on which a group
, on which a group  acts, for instance the group of Euclidean motions, then the isotropy subgroup
acts, for instance the group of Euclidean motions, then the isotropy subgroup  of
of  is the symmetry group of the structure
is the symmetry group of the structure  .
.
References
| [a1] | L. Michel, "Simple mathematical models for symmetry breaking" K. Maurin (ed.) R. Raczka (ed.) , Mathematical Physics and Physical Mathematics , Reidel (1976) pp. 251–262 |
| [a2] | S. Helgason, "Differential geometry, Lie groups, and symmetric spaces" , Acad. Press (1978) pp. 121 |
| [a3] | T. Petrie, J.D. Randall, "Transformation groups on manifolds" , M. Dekker (1984) pp. 8, 9 |
Stabilizer. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stabilizer&oldid=19013