Stability theorems in algebraic K-theory
Assertions on the invariance of the groups 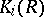 or their subgroups, given certain special extensions of the ground ring
or their subgroups, given certain special extensions of the ground ring  (see Algebraic
(see Algebraic 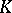 -theory).
-theory).
The following are the best-known stability theorems. Let 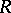 be a regular ring (cf. Regular ring (in commutative algebra)) and let
be a regular ring (cf. Regular ring (in commutative algebra)) and let 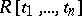 be the ring of polynomials in the variables
be the ring of polynomials in the variables  over
over  . The stability theorem for Whitehead groups under the transfer from
. The stability theorem for Whitehead groups under the transfer from 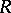 to
to 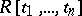 , [1], states that the natural homomorphism imbedding
, [1], states that the natural homomorphism imbedding 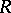 in
in 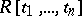 induces an isomorphism between
induces an isomorphism between 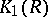 and
and 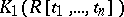 (cf. also Whitehead group).
(cf. also Whitehead group).
In the case of a skew-field 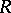 that is finite-dimensional over its centre
that is finite-dimensional over its centre 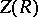 , one can define a reduced-norm homomorphism
, one can define a reduced-norm homomorphism  of the multiplicative group
of the multiplicative group 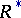 of
of 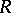 into the multiplicative group
into the multiplicative group 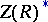 of its centre. The kernel of this homomorphism, usually written as
of its centre. The kernel of this homomorphism, usually written as 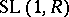 , determines the reduced Whitehead group
, determines the reduced Whitehead group 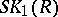 of
of 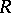 :
:
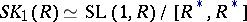 |
(see Special linear group), which is a subgroup in 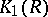 . If
. If 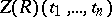 is the field of rational functions in
is the field of rational functions in  over
over 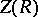 , then the algebra
, then the algebra
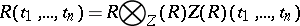 |
is a skew-field, and the natural imbedding 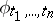 of
of  in
in 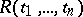 induces a homomorphism
induces a homomorphism
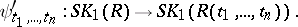 |
The stability theorem for reduced Whitehead groups states that the homomorphism 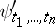 is bijective ([2], see also [3]). Similar statements are also true in unitary and spinor algebraic
is bijective ([2], see also [3]). Similar statements are also true in unitary and spinor algebraic 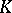 -theories [4], [5].
-theories [4], [5].
Theorems on stabilization for 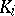 -functors under the transfer from the stable objects
-functors under the transfer from the stable objects 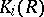 to unstable ones are also called stability theorems (see [6]).
to unstable ones are also called stability theorems (see [6]).
References
| [1] | H. Bass, A. Heller, R. Swan, "The Whitehead group of a polynomial extension" Publ. Math. IHES : 22 (1964) pp. 61–79 |
| [2] | V.P. Platonov, "Reduced 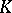 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 -theory and approximation in algebraic groups" Proc. Steklov Inst. Math. , 142 (1976) pp. 213–224 Trudy Mat. Inst. Steklov. , 142 (1976) pp. 198–207 |
| [3] | V.P. Platonov, V.I. Yanchevskii, "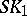 for division rings of noncommutative rational functions" Soviet Math. Dokl. , 20 : 6 (1976) pp. 1393–1397 Dokl. Akad. Nauk SSSR , 249 : 5 (1979) pp. 1064–1068 for division rings of noncommutative rational functions" Soviet Math. Dokl. , 20 : 6 (1976) pp. 1393–1397 Dokl. Akad. Nauk SSSR , 249 : 5 (1979) pp. 1064–1068 |
| [4] | V.I. Yanchevskii, "Reduced unitary 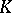 -theory. Applications to algebraic groups" Math. USSR Sb. , 38 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 -theory. Applications to algebraic groups" Math. USSR Sb. , 38 (1981) pp. 533–548 Mat. Sb. , 110 : 4 (1979) pp. 579–596 |
| [5] | A.P. Monastyrnyi, V.I. Yanchevskii, "Whitehead groups of spinor groups" Math. USSR Izv. , 54 : 1 (1991) pp. 61–100 Izv. Akad. Nauk SSSR Ser. Mat. , 54 : 1 (1990) pp. 60–96 |
| [6] | H. Bass, "Algebraic 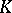 -theory" , Benjamin (1968) -theory" , Benjamin (1968) |
Comments
Many groups in algebraic 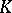 -theory are defined as direct limits. For example, [a1],
-theory are defined as direct limits. For example, [a1], 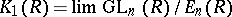 for any associative ring
for any associative ring 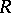 with
with 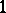 . The corresponding stability theorem asserts that the sequence is eventually stable, i.e., the mappings become isomorphisms starting from some point. In the above example,
. The corresponding stability theorem asserts that the sequence is eventually stable, i.e., the mappings become isomorphisms starting from some point. In the above example, 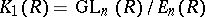 for
for 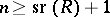 , where
, where 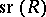 is the Bass stable rank of
is the Bass stable rank of 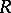 [a1]–[a3]. See [a4] for a similar result for higher
[a1]–[a3]. See [a4] for a similar result for higher 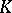 -functors. For the
-functors. For the 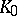 -functor, a stability result is the so-called cancellation theorem [a1]. A similar result for modules with quadratic forms is known as the Witt theorem.
-functor, a stability result is the so-called cancellation theorem [a1]. A similar result for modules with quadratic forms is known as the Witt theorem.
The most common meaning of "stability theorem" is that given in the last sentence of the main article above (i.e. stabilization of 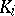 -functors under transfer from stable to unstable objects), cf. [a3].
-functors under transfer from stable to unstable objects), cf. [a3].
The stability theorem for Whitehead groups, or Bass–Heller–Swan theorem, was generalized to all 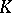 -groups by D. Quillen, [a4].
-groups by D. Quillen, [a4].
References
| [a1] | H. Bass, "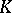 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 485–544 -theory and stable algebra" Publ. Math. IHES , 22 (1964) pp. 485–544 |
| [a2] | L.N. Vaserstein, "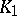 -theory and the congruence subgroup problem" Math. Notes , 5 (1969) pp. 141–148 Mat. Zametki , 5 (1969) pp. 233–244 -theory and the congruence subgroup problem" Math. Notes , 5 (1969) pp. 141–148 Mat. Zametki , 5 (1969) pp. 233–244 |
| [a3] | A. Suslin, "Stability in algebraic 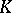 -theory" R.K. Dennis (ed.) , Algebraic -theory" R.K. Dennis (ed.) , Algebraic 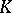 -theory (Oberwolfach, 1980) , Lect. notes in math. , 966 , Springer (1982) pp. 304–333 -theory (Oberwolfach, 1980) , Lect. notes in math. , 966 , Springer (1982) pp. 304–333 |
| [a4] | D. Quillen, "Higher algebraic  -theory I" H. Bass (ed.) , Algebraic -theory I" H. Bass (ed.) , Algebraic 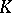 -theory I (Battelle Inst. Conf.) , Lect. notes in math. , 341 , Springer (1973) pp. 85–147 -theory I (Battelle Inst. Conf.) , Lect. notes in math. , 341 , Springer (1973) pp. 85–147 |
Stability theorems in algebraic K-theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_theorems_in_algebraic_K-theory&oldid=12794