Stability of a computational process
A property characterizing the speed of accumulation of gross computing errors. The concept of stability of a computational process was introduced because in real calculations one cannot operate with exact numbers and it is impossible to circumvent rounding, which is sometimes the cause of a fast loss of accuracy.
A computational process is a sequence of arithmetic operations on numbers. Let 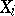 be a normed linear space and
be a normed linear space and  a continuous operator
a continuous operator  . Then the sequence of equations
. Then the sequence of equations
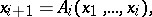 | (1) |
 |
gives a computational process with original data  and intermediate results
and intermediate results  ,
,  . Usually
. Usually  and the operator
and the operator 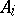 consists of a finite number of arithmetic operations. As a rule
consists of a finite number of arithmetic operations. As a rule  depends not on all the intermediate results obtained earlier. The number
depends not on all the intermediate results obtained earlier. The number 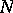 may be given in advance or determined in the course of the computational process itself. In the latter case
may be given in advance or determined in the course of the computational process itself. In the latter case 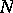 depends on
depends on  (e.g. if
(e.g. if  is the number of iterations needed for a given degree of accuracy).
is the number of iterations needed for a given degree of accuracy).
An actual computational process may not be carried out exactly in conformity with definition (1), because in carrying out the arithmetic operations rounding errors are introduced and 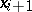 may be obtained from inexact previous results. This means that instead of
may be obtained from inexact previous results. This means that instead of  one has actually calculated the element
one has actually calculated the element
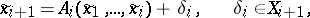 | (2) |
where the small additive error 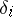 arises by rounding in the course of applying the operator
arises by rounding in the course of applying the operator 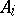 . The value of
. The value of  , determined from the values of
, determined from the values of 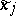 ,
, 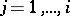 , depends on the method of rounding, the working of the machine program, etc. However, even if
, depends on the method of rounding, the working of the machine program, etc. However, even if  is small for
is small for  , this by itself will not guarantee that
, this by itself will not guarantee that 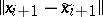 is small. This difference will be small only for a so-called stable computational process, for which it is not strongly dependent on
is small. This difference will be small only for a so-called stable computational process, for which it is not strongly dependent on 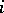 .
.
References
| [1] | I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Numerical processes in differential equations" , Wiley (1966) |
| [2] | V.V. Voevodin, "Rounding-off errors and stability in direct methods of linear algebra" , Moscow (1969) (In Russian) |
| [3] | M.K. Gavurin, "Lectures on computing methods" , Moscow (1971) (In Russian) |
Comments
References
| [a1] | J.H. Wilkinson, "Rounding errors in algebraic processes" , Prentice-Hall (1963) |
Stability of a computational process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_of_a_computational_process&oldid=16612