Stability of a computational algorithm
A partially resolving operator 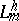 , uniformly bounded in
, uniformly bounded in 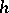 and
and 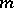 , describing the succession of steps in the computational algorithm for solving the equation
, describing the succession of steps in the computational algorithm for solving the equation
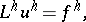 |
for example, a grid equation with step 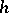 (cf. Closure of a computational algorithm). Stability of a computational algorithm guarantees weak influence of computational errors on the result of the calculation. However, the possibility is not excluded that the quantity
(cf. Closure of a computational algorithm). Stability of a computational algorithm guarantees weak influence of computational errors on the result of the calculation. However, the possibility is not excluded that the quantity 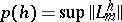 grows comparatively slowly and a corresponding strengthening of the influence of computational errors for
grows comparatively slowly and a corresponding strengthening of the influence of computational errors for 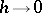 remains practically admissible. The concept of stability of a computational algorithm has been made concrete in applications to grid-projection methods (cf. [4]) and in applications to iterative methods (cf. [6]). There are also other definitions of the stability of a computational algorithm (cf. e.g. [1], [3]).
remains practically admissible. The concept of stability of a computational algorithm has been made concrete in applications to grid-projection methods (cf. [4]) and in applications to iterative methods (cf. [6]). There are also other definitions of the stability of a computational algorithm (cf. e.g. [1], [3]).
References
| [1] | I. [I. Babushka] Babuška, M. Práger, E. Vitásek, "Numerical processes in differential equations" , Wiley (1966) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [3] | M.K. Gavurin, "Lectures on computing methods" , Moscow (1971) (In Russian) |
| [4] | G.I. Marchuk, V.I. Agoshkov, "Introduction to grid-projection methods" , Moscow (1981) (In Russian) |
| [5] | A.A. Samarskii, A.V. Gulin, "Stability of difference schemes" , Moscow (1973) (In Russian) |
| [6] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian) |
Stability of a computational algorithm. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stability_of_a_computational_algorithm&oldid=19109