Spray
on a differentiable manifold 
A vector field  on the tangent space
on the tangent space  which, in terms of the local coordinates
which, in terms of the local coordinates  on
on  associated in a natural way with the local coordinates
associated in a natural way with the local coordinates  on
on  , has components
, has components  , where
, where  are functions of class
are functions of class  which are, for fixed
which are, for fixed  , positive homogeneous functions in
, positive homogeneous functions in  of degree 2 (these properties of
of degree 2 (these properties of  do not depend on the actual choice of the local coordinates). The system of differential equations determined by this vector field,
do not depend on the actual choice of the local coordinates). The system of differential equations determined by this vector field,
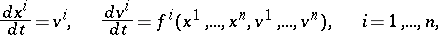 |
is equivalent to the system of second-order differential equations
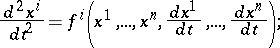 |
therefore a spray describes (and moreover in an invariant manner, that is, independent of the coordinate system) a system of such equations on  .
.
The most important case of a spray is when the  are polynomials of the second degree in the
are polynomials of the second degree in the  :
:
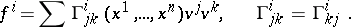 | (*) |
In this case the  give an affine connection on
give an affine connection on  with zero torsion tensor. Conversely, for every affine connection the equations of the geodesic lines are given by a certain spray with
with zero torsion tensor. Conversely, for every affine connection the equations of the geodesic lines are given by a certain spray with 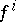 of the form (*) (where when going from the connection to the spray, the
of the form (*) (where when going from the connection to the spray, the  symmetrize with respect to the suffixes). If the field
symmetrize with respect to the suffixes). If the field 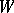 is of class
is of class 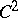 , then
, then  must have the form (*). In the general case, however,
must have the form (*). In the general case, however,  may be smooth outside the zero section of the bundle
may be smooth outside the zero section of the bundle  , but need not be a field of class
, but need not be a field of class  near this section. In such a situation one sometimes talks about a generalized spray, leaving the term "spray" only for the special case (*). The differential equations for geodesics in Finsler geometry give rise to a generalized spray.
near this section. In such a situation one sometimes talks about a generalized spray, leaving the term "spray" only for the special case (*). The differential equations for geodesics in Finsler geometry give rise to a generalized spray.
It is possible to give a definition of a spray in invariant terms, which is suitable also for Banach manifolds (see [1]).
References
| [1] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) |
Comments
The spray of an affine connection is also called the geodesic spray of this connection.
References
| [a1] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
Spray. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spray&oldid=13449