Spline interpolation
Interpolation by means of splines (cf. Spline), that is, the construction of an interpolation spline taking given values  at prescribed points
at prescribed points  ,
,  . Interpolation splines usually satisfy further conditions at the end points. E.g., for the cubic spline
. Interpolation splines usually satisfy further conditions at the end points. E.g., for the cubic spline  , where
, where  is the partition
is the partition  , which, on
, which, on  , consists of piecewise-cubic polynomials and has a continuous second-order derivative, one requires that
, consists of piecewise-cubic polynomials and has a continuous second-order derivative, one requires that 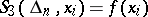 and, in addition, one condition at each end point (e.g.,
and, in addition, one condition at each end point (e.g.,  and
and 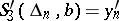 , or
, or 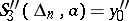 and
and 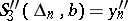 ). If the
). If the  are the values of a
are the values of a 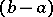 -periodic function, then one requires the spline to be
-periodic function, then one requires the spline to be 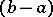 -periodic also. For polynomial splines of degree
-periodic also. For polynomial splines of degree 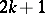 , the number of extra conditions at each end point
, the number of extra conditions at each end point  or
or 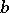 is increased by
is increased by 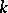 . For interpolation splines of degree
. For interpolation splines of degree  , the knots of the spline (the points of discontinuity of the
, the knots of the spline (the points of discontinuity of the  -th derivative) are usually chosen halfway between the points
-th derivative) are usually chosen halfway between the points  , and a further
, and a further  conditions are assigned at
conditions are assigned at  and
and  .
.
Spline interpolation has some advantages when compared to polynomial interpolation. E.g., there are sequences of partitions 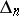 :
:  and interpolation splines for which the interpolation process converges for any continuous function, provided that
and interpolation splines for which the interpolation process converges for any continuous function, provided that
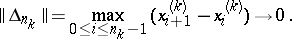 |
Many processes of spline interpolation give the same order of approximation as the best approximation. Moreover, spline interpolation of some classes of differentiable functions has the property that the error does not exceed the width of the corresponding class. Spline interpolation can be used to solve certain variational problems. E.g., under sufficiently general additional conditions at  and
and  , interpolation splines satisfy the relation:
, interpolation splines satisfy the relation:
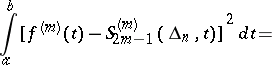 | (1) |
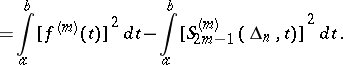 |
This implies the existence and uniqueness of interpolation splines of odd degree, and also the simplest results on convergence:
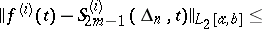 | (2a) |
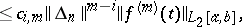 |
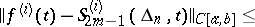 | (2b) |
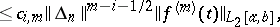 |
 , where the
, where the  depend only on
depend only on 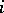 and
and 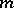 , and
, and 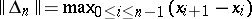 . For some classes of differentiable functions, the sequence of interpolation splines converges to the function to be interpolated on any sequence of partitions
. For some classes of differentiable functions, the sequence of interpolation splines converges to the function to be interpolated on any sequence of partitions  for which
for which  (this occurs in case (2a)–(2b)).
(this occurs in case (2a)–(2b)).
In addition to polynomial interpolation splines, one can also use splines of a more general form (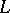 -splines or
-splines or  -splines). For many of these, results analogous to (1) and (2a)–(2b) also hold. For splines with defect greater than 1 one usually carries out interpolation with multiple knots.
-splines). For many of these, results analogous to (1) and (2a)–(2b) also hold. For splines with defect greater than 1 one usually carries out interpolation with multiple knots.
See also Spline approximation.
For references see Spline.
Comments
References
| [a1] | T. Lyche, L.L. Schumaker, "On the convergence of cubic interpolating splines" A. Meir (ed.) A. Sharma (ed.) , Spline Functions and Approximation Theory , Birkhäuser (1973) pp. 169–189 |
| [a2] | Yu.N. Subbotin, "Interpolating splines" Z. Cieselski (ed.) J. Musielak (ed.) , Approximation Theory , Reidel (1975) pp. 221–234 |
| [a3] | I.J. Schoenberg, "Cardinal spline interpolation" , SIAM (1973) |
| [a4] | P.M. Prenter, "Splines and variational methods" , Wiley (1975) |
Spline interpolation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spline_interpolation&oldid=11892