Spline
A function  which is defined and has continuous
which is defined and has continuous 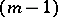 -st derivative on an interval
-st derivative on an interval 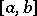 , and which coincides on each interval
, and which coincides on each interval 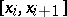 formed by the partition
formed by the partition 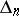 :
: 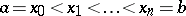 with a certain algebraic polynomial of degree at most
with a certain algebraic polynomial of degree at most 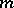 . Splines can be represented in the following way:
. Splines can be represented in the following way:
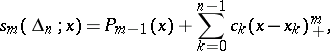 |
where the 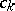 are real numbers,
are real numbers, 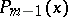 is a polynomial of degree at most
is a polynomial of degree at most 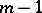 , and
, and 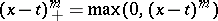 . The points
. The points 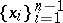 are called the knots of the spline. If a spline
are called the knots of the spline. If a spline 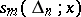 has a continuous
has a continuous 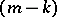 -th derivative on
-th derivative on 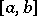 for
for 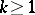 and at the knots the
and at the knots the 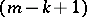 -st derivative of the spline is discontinuous, then it is said to have defect
-st derivative of the spline is discontinuous, then it is said to have defect 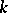 . Besides these polynomial splines, one also considers more general splines (
. Besides these polynomial splines, one also considers more general splines (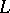 -splines), which are "tied together" from solutions of a homogeneous linear differential equation
-splines), which are "tied together" from solutions of a homogeneous linear differential equation 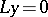 , splines (
, splines (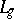 -splines) with different smoothness properties at various knots, and also splines in several variables. Splines and their generalizations often occur as extremal functions when solving extremum problems, e.g. in obtaining best quadrature formulas and best numerical differentiation formulas. Splines are applied to approximate functions (see Spline approximation; Spline interpolation), and in constructing approximate solutions of ordinary and partial differential equations. They can also be used to construct orthonormal systems with good convergence properties.
-splines) with different smoothness properties at various knots, and also splines in several variables. Splines and their generalizations often occur as extremal functions when solving extremum problems, e.g. in obtaining best quadrature formulas and best numerical differentiation formulas. Splines are applied to approximate functions (see Spline approximation; Spline interpolation), and in constructing approximate solutions of ordinary and partial differential equations. They can also be used to construct orthonormal systems with good convergence properties.
References
| [1] | S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian) |
Comments
I.J. Schoenberg is generally acknowledged to be the "father" of splines; these functions were named and singled out for special study by him in the middle of the 1940's. Since 1960 the field of spline interpolation and approximation has grown enormously. For a reasonably complete bibliography of papers dealing with spline functions that were published before 1973, see [a4]; a valuable bibliography is also contained in [a3].
References
| [a1] | I.J. Schoenberg, "Contributions to the problem of approximation of equidistant data by analytic functions. Part A: On the problem of smoothing of graduation. A first class of analytic approximation formulae" Quart. Appl Math. , 4 (1946) pp. 45–99 |
| [a2] | I.J. Schoenberg, "Contributions to the problem of approximation of equidistant data by analytic functions. Part B: On the problem of osculatory formulae" Quart. Appl. Math. , 4 (1946) pp. 112–141 |
| [a3] | L.L. Schumaker, "Spline functions, basic theory" , Wiley (1981) |
| [a4] | F. Schurer, "A bibliography on spline functions" K. Böhmer (ed.) G. Meinardus (ed.) W. Schempp (ed.) , Spline-Funktionen , B.I. Wissenschaftsverlag Mannheim (1974) pp. 315–415 |
| [a5] | P.M. Prenter, "Splines and variational methods" , Wiley (1975) |
Spline. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spline&oldid=15640