Spherical indicatrix
The image of a curve in the three-dimensional Euclidean space 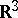 under a mapping from the points of the curve onto the unit sphere
under a mapping from the points of the curve onto the unit sphere 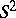 by any of the following unit vectors: the tangent, the principal normal or the binormal of this curve. Let
by any of the following unit vectors: the tangent, the principal normal or the binormal of this curve. Let 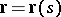 be the radius vector of the curve
be the radius vector of the curve 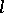 , let
, let  be the natural parameter and let
be the natural parameter and let 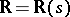 be the radius vector of the spherical mapping of the curve
be the radius vector of the spherical mapping of the curve 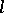 into the unit sphere
into the unit sphere 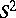 with its centre at the origin by means of one of the unit vectors listed. The equation of the spherical indicatrix of the tangent is defined by the equation
with its centre at the origin by means of one of the unit vectors listed. The equation of the spherical indicatrix of the tangent is defined by the equation
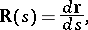 |
that of the spherical indicatrix of the principal normal by the equation
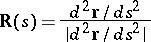 |
and that of the spherical indicatrix of the binormal by the equation
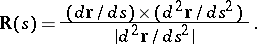 |
The tangent to the spherical indicatrix of the tangent is parallel to the principal normal of the curve at the corresponding values  . The curvature and the torsion of the spherical indicatrix can be expressed in terms of the curvature and torsion of the curve itself. For every spherical indicatrix there is an infinite set of curves for which it is an indicatrix, i.e. a curve cannot be uniquely restored from its spherical indicatrix.
. The curvature and the torsion of the spherical indicatrix can be expressed in terms of the curvature and torsion of the curve itself. For every spherical indicatrix there is an infinite set of curves for which it is an indicatrix, i.e. a curve cannot be uniquely restored from its spherical indicatrix.
References
| [1] | M.Ya. Vygodskii, "Differential geometry" , Moscow-Leningrad (1949) (In Russian) |
Comments
References
| [a1] | D.J. Struik, "Differential geometry" , Addison-Wesley (1957) |
| [a2] | C.E. Weatherburn, "Differential geometry" , 1 , Cambridge Univ. Press (1961) |
| [a3] | G. Salmon, "Analytische Geometrie des Raumes" , 1–2 , Teubner (1898) |
Spherical indicatrix. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spherical_indicatrix&oldid=17468