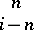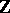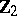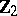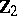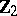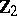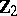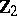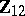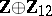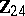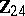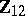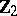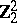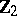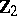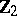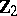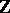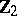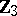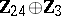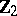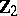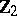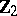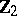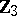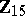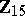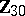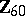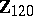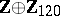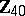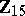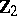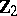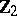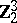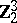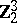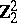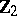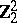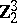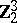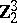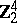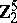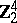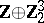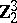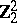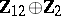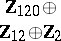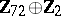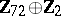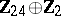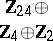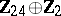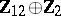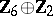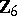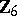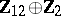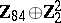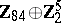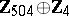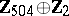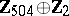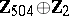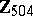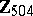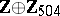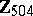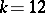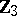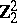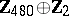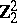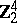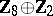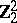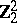Spheres, homotopy groups of the
An object of study in classical homotopy theory. The calculation of the homotopy groups of the spheres, 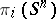 , was considered in its time (especially in the 1950's) as one of the central problems in topology. Topologists hoped that these groups could be successfully calculated completely, and that they would help to solve other classification problems in homotopy. These hopes were not to be realized in full: The homotopy groups of the spheres could only be calculated partially, and with the development of generalized cohomology theories, the problem of their calculation became less pressing. However, all the information that had been compiled on these groups was not wasted, as it found an unexpected use in differential topology (the classification of differential structures on spheres and multi-dimensional knots).
, was considered in its time (especially in the 1950's) as one of the central problems in topology. Topologists hoped that these groups could be successfully calculated completely, and that they would help to solve other classification problems in homotopy. These hopes were not to be realized in full: The homotopy groups of the spheres could only be calculated partially, and with the development of generalized cohomology theories, the problem of their calculation became less pressing. However, all the information that had been compiled on these groups was not wasted, as it found an unexpected use in differential topology (the classification of differential structures on spheres and multi-dimensional knots).
I. General theory.
1) If 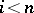 or
or 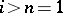 , then
, then 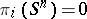 .
.
2)  (the Brouwer–Hopf theorem); this isomorphism relates an element of the group
(the Brouwer–Hopf theorem); this isomorphism relates an element of the group  to the degree of the mapping
to the degree of the mapping 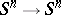 representing it.
representing it.
3) The groups 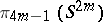 have rank 1; the other groups
have rank 1; the other groups 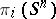 with
with 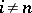 are finite.
are finite.
The suspension homomorphism
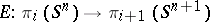 |
relates an element of the group 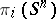 , represented by the mapping
, represented by the mapping 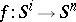 , to the class of the mapping
, to the class of the mapping 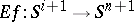 , defined by the formula
, defined by the formula
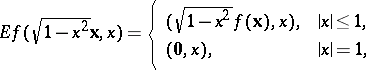 |
where 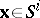 ,
, 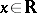 .
.
4) The homomorphism 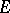 is an isomorphism when
is an isomorphism when 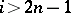 , and an epimorphism when
, and an epimorphism when 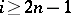 .
.
Thus, for every 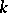 the groups
the groups 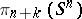 can be made terms of a sequence
can be made terms of a sequence
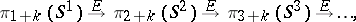 |
at the 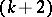 -nd term of which stabilization begins; the groups
-nd term of which stabilization begins; the groups 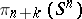 with
with 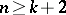 are called the
are called the 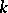 -th stable homotopy groups of the spheres, and are denoted by
-th stable homotopy groups of the spheres, and are denoted by 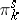 . Then
. Then 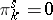 when
when 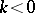 and
and 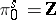 .
.
As for the homotopy groups (cf. Homotopy group) of any topological space, the Whitehead product is defined on the homotopy groups of the spheres:
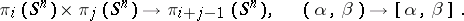 |
To its usual properties (distributivity, skew commutativity and the Jacobi identity) is added
5) 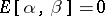 .
.
The Whitehead product enables one to make the following refinement to 4):
6) The kernel of the epimorphism 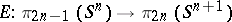 is generated by the class
is generated by the class 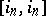 , where
, where 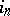 is a canonical generator of the group
is a canonical generator of the group 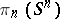 (representable by the identity mapping).
(representable by the identity mapping).
Closely linked to the Whitehead product is the Hopf invariant 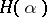 , defined for
, defined for 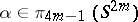 . Thus, the element of the group
. Thus, the element of the group 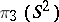 which can be represented by the Hopf mapping
which can be represented by the Hopf mapping 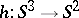 that operates according to the formula
that operates according to the formula 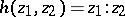 (in which
(in which 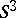 is interpreted as the unit sphere in the space
is interpreted as the unit sphere in the space 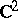 , while
, while 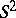 is interpreted as
is interpreted as  ) has Hopf invariant equal to 1.
) has Hopf invariant equal to 1.
7) The mapping 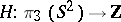 is an isomorphism.
is an isomorphism.
8) 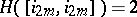 .
.
A consequence of 8) is that the groups 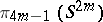 are infinite, a fact already stated in 3).
are infinite, a fact already stated in 3).
9) When 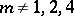 , in
, in 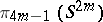 there are no elements of odd Hopf invariant (as was known long before this theorem was proved, its assertion is equivalent to the following Frobenius conjecture: when
there are no elements of odd Hopf invariant (as was known long before this theorem was proved, its assertion is equivalent to the following Frobenius conjecture: when 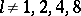 , then in
, then in 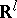 there is no bilinear multiplication with single-valued division on non-zero elements).
there is no bilinear multiplication with single-valued division on non-zero elements).
The composition product
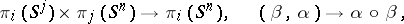 |
which can be defined by juxtaposition of mappings, is unique to the spheres.
10) For any 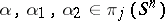 ,
, 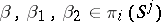 ,
, 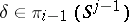 ,
, 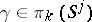 , the following hold:
, the following hold:
a) 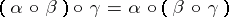 ;
;
b) 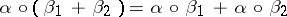 ;
;
c)  ;
;
d) 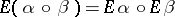 .
.
The "left law of distributivity" ,  , generally speaking, does not hold. Assertion d) enables one to define a stable composition product
, generally speaking, does not hold. Assertion d) enables one to define a stable composition product
 |
11) For any  ,
, 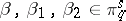 ,
, 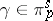 , assertions a) and b) in 10) hold, as do:
, assertions a) and b) in 10) hold, as do:
c') 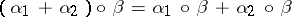 ,
,
d') 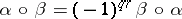 .
.
II. Methods of calculation.
The geometric method of L.S. Pontryagin (see [1]), proposed in the mid-1930s, is based on the following definition. A smooth 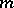 -dimensional compact manifold
-dimensional compact manifold 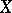 in
in 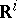 is said to be framed if a smooth field of
is said to be framed if a smooth field of 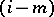 -frames transversal to it is defined on the manifold; the field itself is said to be a framing. Two framed manifolds
-frames transversal to it is defined on the manifold; the field itself is said to be a framing. Two framed manifolds 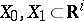 , without boundary, are said to be cobordant if there exists a framed manifold
, without boundary, are said to be cobordant if there exists a framed manifold 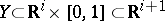 with
with 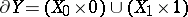 for which the restriction of the framing onto
for which the restriction of the framing onto 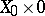 and
and 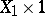 is contained in
is contained in 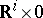 and
and 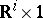 , and, given a natural identification of
, and, given a natural identification of  and
and 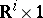 with
with 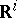 , is turned into the given framing of the manifolds
, is turned into the given framing of the manifolds 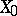 and
and 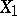 . The set of classes of cobordant framed
. The set of classes of cobordant framed 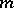 -dimensional manifolds without boundary in
-dimensional manifolds without boundary in 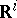 is denoted by
is denoted by 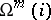 .
.
1) There is a one-to-one correspondence between 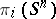 and
and  .
.
This method gives good results for small 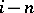 . It also makes it possible to prove certain of the theorems in section I and provides a variety of geometric information on manifolds of small dimensions.
. It also makes it possible to prove certain of the theorems in section I and provides a variety of geometric information on manifolds of small dimensions.
Another group of methods consists of elementary algebraic methods comprising the use of homotopy sequences of various fibre bundles, properties of the Whitehead product, the composition product, and the corresponding higher product (Toda brackets, see [3]), as well as the following theorem of James.
2) There is a sequence of groups and homomorphisms
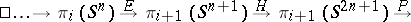 |
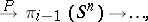 |
which is exact for odd  and for
and for 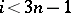 (in this sequence,
(in this sequence,  is a generalization of the Hopf invariant).
is a generalization of the Hopf invariant).
Elementary algebraic methods prove to be reasonable effective: It is possible to calculate the groups 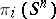 when
when 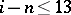 almost without having to resort to other methods.
almost without having to resort to other methods.
There is also the method of killing spaces (see [5] and Killing space). This method is suitable for the calculation of the homotopy groups of any space. It is based on the construction, using a space 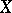 , of a sequence of killing spaces
, of a sequence of killing spaces 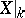 with the following property:
with the following property:
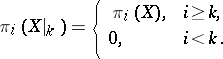 |
Thus, 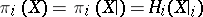 and the problem of calculating the homotopy groups reduces to the problem of calculating the homology groups (and the cohomology groups) of
and the problem of calculating the homotopy groups reduces to the problem of calculating the homology groups (and the cohomology groups) of 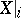 . These homology groups are found by induction, using spectral sequences (cf. Spectral sequence) of fibre bundles:
. These homology groups are found by induction, using spectral sequences (cf. Spectral sequence) of fibre bundles: 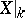 is broken down with fibre
is broken down with fibre 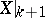 over the Eilenberg–MacLane space
over the Eilenberg–MacLane space 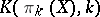 . The calculation does not have an automatic character: In order to progress, it is necessary to know as much as possible about the cohomology groups of
. The calculation does not have an automatic character: In order to progress, it is necessary to know as much as possible about the cohomology groups of 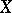 , including the action in them of the primary and the higher cohomology operations (cf. Cohomology operation).
, including the action in them of the primary and the higher cohomology operations (cf. Cohomology operation).
A more suitable apparatus for calculating the stable homotopy groups of the spheres is the Adams spectral sequence. Let 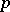 be a prime number, and let
be a prime number, and let 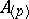 be the Steenrod algebra of stable cohomology operations on the cohomology spaces with coefficients in
be the Steenrod algebra of stable cohomology operations on the cohomology spaces with coefficients in 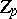 .
.
3) There exists a spectral sequence the first term of which coincides with the cohomology groups of the Steenrod algebra (i.e. with 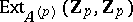 ), while the limit term is related to the stable homotopy groups of the spheres factored by the torsion of order relatively prime to
), while the limit term is related to the stable homotopy groups of the spheres factored by the torsion of order relatively prime to 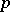 .
.
The Adams spectral sequence permits one to achieve considerable progress in the calculation of the stable homotopy groups of the spheres. An analogous spectral sequence exists for the calculation of the stable homotopy groups of any space. There is also an unstable analogue of the Adams spectral sequence (see [4]).
More modern methods of calculating the homotopy groups of the spheres are based on generalized cohomology theories. One of these involves the use of the Adams'  -invariant, which is closely linked to
-invariant, which is closely linked to 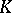 -theory. In constructing this
-theory. In constructing this  -invariant, a mapping
-invariant, a mapping 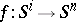 representing a class
representing a class 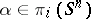 is fixed, and the space
is fixed, and the space 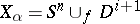 , obtained by attaching an
, obtained by attaching an 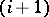 -dimensional cell to the sphere
-dimensional cell to the sphere 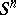 through the mapping
through the mapping 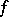 , is examined. It turns out that
, is examined. It turns out that
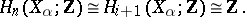 |
Let 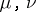 be the canonical generators of these groups. There exists a complex vector bundle
be the canonical generators of these groups. There exists a complex vector bundle 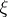 over
over 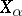 with Chern character
with Chern character 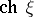 satisfying the relation
satisfying the relation 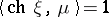 . Then
. Then 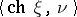 is a rational number, the residue of which modulo 1 does not depend on the choice of
is a rational number, the residue of which modulo 1 does not depend on the choice of 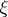 . This residue is the
. This residue is the  -invariant
-invariant 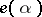 of the class
of the class 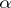 . The function
. The function  is a homomorphism
is a homomorphism
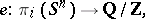 |
whose image can be determined (see ).
Finally, the potentially most powerful method of calculating the homotopy groups of the spheres (and not only of the spheres) is the Adams–Novikov spectral sequence, an analogue of the Adams spectral sequence, constructed on the basis not of ordinary cohomology groups, but of cobordisms. However, an explicit calculation of the first term of this sequence has inherent difficulties, which have not been overcome yet (1984).
III. Results of calculations.
1) The groups 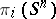 with
with 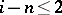 are isomorphic to the groups from the following table:'
are isomorphic to the groups from the following table:'
<tbody> </tbody>
|
2) The groups 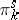 with
with 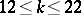 are isomorphic to the groups from the following table:'
are isomorphic to the groups from the following table:'
<tbody> </tbody>
|
For further results on the calculation of the groups 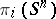 , see [3]. Particular progress has been achieved in the calculation of the odd primary components of these groups.
, see [3]. Particular progress has been achieved in the calculation of the odd primary components of these groups.
For example:
3) If 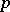 is an odd prime number, then the
is an odd prime number, then the 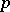 -primary component of the group
-primary component of the group 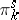 is
is  when
when 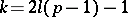 ,
, 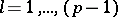 , and is trivial for other
, and is trivial for other 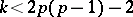 .
.
There are many results concerning the homotopy groups of the spheres, the domain of action of which is not restricted by any finite range of values 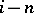 . In particular, a large number of infinite series of non-trivial elements of the groups
. In particular, a large number of infinite series of non-trivial elements of the groups 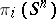 is known (see [4]).
is known (see [4]).
4) The order of the image of the Whitehead homomorphism 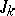 is equal to the denominator of the irreducible fraction equal to
is equal to the denominator of the irreducible fraction equal to 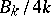 , where
, where 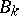 is the
is the 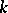 -th Bernoulli number (cf. Bernoulli numbers). In particular,
-th Bernoulli number (cf. Bernoulli numbers). In particular, 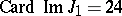 ,
, 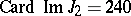 ,
, 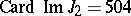 ,
, 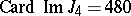 .
.
References
| [1] | L.S. Pontryagin, "Smooth manifolds and their applications in homotopy theory" , Moscow (1976) (In Russian) |
| [2a] | J. Adams, "On the groups  I" Topology , 2 (1963) pp. 181–195 I" Topology , 2 (1963) pp. 181–195 |
| [2b] | J. Adams, "On the groups 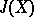 II" Topology , 3 (1966) pp. 137–181 II" Topology , 3 (1966) pp. 137–181 |
| [2c] | J. Adams, "On the groups 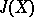 III" Topology , 3 (1966) pp. 193–222 III" Topology , 3 (1966) pp. 193–222 |
| [2d] | J. Adams, "On the groups 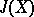 IV" Topology , 5 (1966) pp. 21–71 IV" Topology , 5 (1966) pp. 21–71 |
| [3] | H. Toda, "Composition methods in homotopy groups of spheres" , Princeton Univ. Press (1962) |
| [4] | G.W. Whitehead, "Recent advances in homotopy theory" , Amer. Math. Soc. (1970) |
| [5] | D.B. Fuks, A.T. Fomenko, V.L. Gutenmakher, "Homotopic topology" , Moscow (1969) (In Russian) |
Comments
The general results 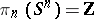 ,
, 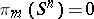 for
for 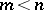 are also together termed the Hurewicz theorem. The fact that the suspension induces an isomorphism in the appropriate range is known as the Freudenthal suspension theorem. The result that the
are also together termed the Hurewicz theorem. The fact that the suspension induces an isomorphism in the appropriate range is known as the Freudenthal suspension theorem. The result that the 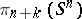 ,
, 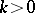 , are finite except for the
, are finite except for the 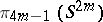 , which are of the form
, which are of the form 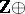 (finite), is known as Serre's finiteness theorem. An additional result pertaining to the composition product is the Nishida nilpotence theorem that each
(finite), is known as Serre's finiteness theorem. An additional result pertaining to the composition product is the Nishida nilpotence theorem that each 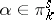 ,
, 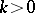 , is nilpotent. Further, there is the Cohen–Moore–Neisendorfer exponent theorem, which says that for
, is nilpotent. Further, there is the Cohen–Moore–Neisendorfer exponent theorem, which says that for 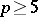 the
the 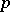 -component of the Abelian group
-component of the Abelian group 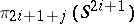 has exponent
has exponent 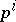 .
.
For a very complete discussion of the homotopy groups of the spheres, and in particular the Adams–Novikov spectral sequence and its 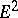 term, cf. [a2].
term, cf. [a2].
References
| [a1] | J. Dieudonné, "A history of algebraic and differential topology 1900–1960" , Birkhäuser (1989) |
| [a2] | D.C. Ravenel, "Complex cobordism and stable homotopy groups of the spheres" , Acad. Press (1986) |
Spheres, homotopy groups of the. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spheres,_homotopy_groups_of_the&oldid=19204