Sphere
The set  of points
of points  of a Euclidean space
of a Euclidean space  that are situated at a constant distance
that are situated at a constant distance  (the radius of the sphere) from a point
(the radius of the sphere) from a point  (the centre of the sphere), i.e.
(the centre of the sphere), i.e.
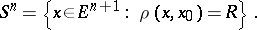 |
The sphere  is a pair of points, the sphere
is a pair of points, the sphere  is the circle, the sphere
is the circle, the sphere  , when
, when 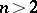 , is sometimes called a hypersphere. The volume of the sphere
, is sometimes called a hypersphere. The volume of the sphere 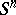 (the length when
(the length when  , the surface when
, the surface when  ) is given by the formula
) is given by the formula
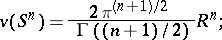 |
in particular,
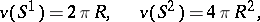 |
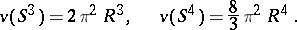 |
Here 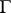 is the gamma-function.
is the gamma-function.
The equation of a sphere  in the Cartesian coordinates of
in the Cartesian coordinates of 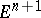 takes the form
takes the form
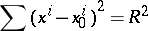 |
(here 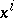 ,
,  ,
,  , are the coordinates of
, are the coordinates of 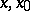 respectively), i.e. the sphere is a (hyper-)quadric or a surface of the second order of special form.
respectively), i.e. the sphere is a (hyper-)quadric or a surface of the second order of special form.
The position of any point in space relative to a sphere is characterized by the power of the point (cf. Degree of a point). The totality of all spheres (in  -space) relative to which a given point has a fixed power forms a web of spheres. The totality of all spheres relative to which the points of a straight line (the radical axis) have an identical power (different for different points), forms a net of spheres. The totality of all spheres relative to which the points of a plane (the radical plane) have an identical degree (different for different points), forms a pencil of spheres.
-space) relative to which a given point has a fixed power forms a web of spheres. The totality of all spheres relative to which the points of a straight line (the radical axis) have an identical power (different for different points), forms a net of spheres. The totality of all spheres relative to which the points of a plane (the radical plane) have an identical degree (different for different points), forms a pencil of spheres.
From the point of view of differential geometry, the sphere 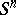 is a Riemannian space of constant curvature
is a Riemannian space of constant curvature 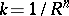 . (This curvature is Gaussian when
. (This curvature is Gaussian when 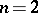 and Riemannian when
and Riemannian when 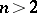 .) All geodesics of a sphere are closed and have constant length
.) All geodesics of a sphere are closed and have constant length  — these are known as great circles, i.e. the intersections with
— these are known as great circles, i.e. the intersections with 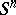 of two-dimensional planes in
of two-dimensional planes in 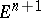 that pass through its centre. The exterior-geometric properties of
that pass through its centre. The exterior-geometric properties of 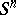 are: all normals intersect at one point; the curvature of any normal section is one and the same and does not depend on the point at which it is examined, in particular, it has constant mean curvature, whereby the complete mean curvature of the sphere is the least among the convex surfaces of identical area; and all points of the sphere are umbilical (cf. Umbilical point).
are: all normals intersect at one point; the curvature of any normal section is one and the same and does not depend on the point at which it is examined, in particular, it has constant mean curvature, whereby the complete mean curvature of the sphere is the least among the convex surfaces of identical area; and all points of the sphere are umbilical (cf. Umbilical point).
Certain of these properties, which are taken to be fundamental, have been used as the starting point for a generalization of the concept of a sphere. For example, an affine sphere is defined by the fact that all its (affine) normals intersect at one point; a pseudo-sphere is a surface in 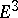 of constant Gaussian curvature (although negative); one of the interpretations of a horosphere (limit sphere) is as the set of points within
of constant Gaussian curvature (although negative); one of the interpretations of a horosphere (limit sphere) is as the set of points within 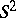 defined by an equation that is also of the second degree:
defined by an equation that is also of the second degree:
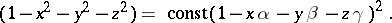 |
The orthogonal group 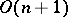 of the space
of the space 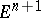 operates doubly-transitive on
operates doubly-transitive on 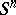 (
( -transitivity means that for any two pairs of points with equal distances between them there is a rotation — an element of
-transitivity means that for any two pairs of points with equal distances between them there is a rotation — an element of 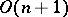 — that maps one pair onto the other); this group is the complete group of isometries of
— that maps one pair onto the other); this group is the complete group of isometries of 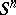 ; finally, a sphere is a homogeneous space:
; finally, a sphere is a homogeneous space: 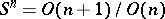 .
.
From the point of view of (differential) topology, the sphere 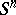 is a closed differentiable manifold that divides
is a closed differentiable manifold that divides 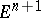 into two domains and that is their common boundary; the bounded domain homeomorphic to
into two domains and that is their common boundary; the bounded domain homeomorphic to 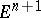 is then an (open) ball; thus, the sphere can be defined as its boundary.
is then an (open) ball; thus, the sphere can be defined as its boundary.
The homology groups of 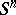 ,
, 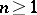 , are:
, are:
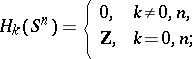 |
in particular,  does not contract into a point, i.e. the identity mapping of
does not contract into a point, i.e. the identity mapping of 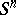 onto itself is essential (cf. Essential mapping).
onto itself is essential (cf. Essential mapping).
The homotopy groups of  ,
, 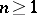 , for
, for  are:
are:
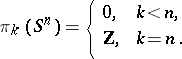 |
In addition one has, for example,  , and
, and  when
when  . Generally, for any
. Generally, for any 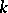 and
and  ,
,  , the groups
, the groups 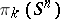 have not been calculated (see Spheres, homotopy groups of the).
have not been calculated (see Spheres, homotopy groups of the).
The concept of a sphere also has a generalization here. For example, a wild sphere is a topological sphere (see below) in 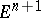 that does not bound a domain homeomorphic to
that does not bound a domain homeomorphic to 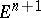 ; a Milnor sphere (an exotic sphere) is a manifold that is homeomorphic, but not diffeomorphic, to
; a Milnor sphere (an exotic sphere) is a manifold that is homeomorphic, but not diffeomorphic, to  .
.
A topological space homeomorphic to a sphere is called a topological sphere. One of the basic problems here is the question of the conditions under which a space is a topological sphere.
Examples. a) No topologically invariant characterization of  when
when  is known (1990). For the case where
is known (1990). For the case where 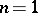 , see One-dimensional manifold. In order that a continuum be homeomorphic to the sphere
, see One-dimensional manifold. In order that a continuum be homeomorphic to the sphere 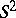 , it is necessary and sufficient that it be locally connected, that it contain at least one simple closed curve and that every such curve that lies in it divides it into two domains having this curve as their common boundary (Wilder's theorem).
, it is necessary and sufficient that it be locally connected, that it contain at least one simple closed curve and that every such curve that lies in it divides it into two domains having this curve as their common boundary (Wilder's theorem).
b) A complete simply-connected Riemannian space of dimension 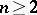 whose curvature
whose curvature  for all tangent two-dimensional planes
for all tangent two-dimensional planes 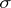 is
is  -bounded with
-bounded with  , i.e.
, i.e. 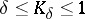 , is homeomorphic to
, is homeomorphic to 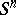 (the sphere theorem, see Riemannian geometry).
(the sphere theorem, see Riemannian geometry).
c) A simply-connected closed smooth manifold whose (integral) homology groups coincide with the homology groups of  is homeomorphic to
is homeomorphic to 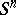 when
when 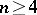 (when
(when  , it is unknown (1990)). If
, it is unknown (1990)). If 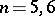 , it is also diffeomorphic to
, it is also diffeomorphic to  (the generalized Poincaré conjecture), when
(the generalized Poincaré conjecture), when 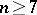 , the diffeomorphism result does not hold.
, the diffeomorphism result does not hold.
A sphere 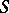 in a metric space
in a metric space  is defined in exactly the same way:
is defined in exactly the same way:  . However, this set, generally speaking, may have a fairly-complicated structure (it may even be empty).
. However, this set, generally speaking, may have a fairly-complicated structure (it may even be empty).
In a normed space  with norm
with norm  , the set
, the set 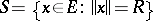 is called a sphere; this is, generally speaking, essentially an arbitrary, infinite-dimensional, convex (hyper)surface, and does not always possess the properties of, for example, smoothness, roundedness and other useful properties of ordinary spheres. One of the variants used in topology — the so-called infinite-dimensional sphere — is the strict inductive limit,
is called a sphere; this is, generally speaking, essentially an arbitrary, infinite-dimensional, convex (hyper)surface, and does not always possess the properties of, for example, smoothness, roundedness and other useful properties of ordinary spheres. One of the variants used in topology — the so-called infinite-dimensional sphere — is the strict inductive limit, 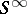 , of a sequence of nested spheres:
, of a sequence of nested spheres:
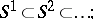 |
another definition: 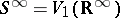 , where
, where  is an infinite-dimensional Stiefel manifold. For any
is an infinite-dimensional Stiefel manifold. For any  , it turns out that
, it turns out that 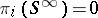 .
.
The applications of the concept of a sphere are remarkably varied. For example, a sphere is used in constructing new spaces or supplementary structures on them. For example, the projective space  can be interpreted as a sphere
can be interpreted as a sphere 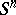 with diametrically-opposite points identified; a sphere with handles and holes is used in handle theory; see also Cohomotopy group; Spherical map.
with diametrically-opposite points identified; a sphere with handles and holes is used in handle theory; see also Cohomotopy group; Spherical map.
References
| [1] | B.A. Rozenfel'd, "Multi-dimensional spaces" , Moscow (1966) (In Russian) |
| [2] | B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian) |
| [3] | P. Lévy, "Problèmes concrets d'analyse fonctionelle" , Gauthier-Villars (1951) |
| [4] | , Introduction to topology , Moscow (1980) (In Russian) |
| [5] | H. Busemann, "The geometry of geodesics" , Acad. Press (1955) |
Comments
A simply-connected topological manifold whose homology is like that of the  -sphere is sometimes called a Poincaré manifold. It was recently shown that a smooth Poincaré
-sphere is sometimes called a Poincaré manifold. It was recently shown that a smooth Poincaré 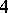 -manifold is not necessarily diffeomorphic to the standard
-manifold is not necessarily diffeomorphic to the standard 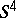 .
.
For a survey of recent results on  -manifolds, including the
-manifolds, including the 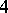 -sphere, see [a3].
-sphere, see [a3].
References
| [a1] | J. Milnor, "On manifolds homeomorphic to the 7-sphere" Ann. of Math. , 64 (1956) pp. 399–405 |
| [a2] | M. Berger, "Geometry" , I , Springer (1977) |
| [a3] | M.H. Freedman, F. Luo, "Selected applications of geometry to low-dimensional topology" , Amer. Math. Soc. (1987) |
Sphere. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sphere&oldid=29439