Spectrum of an element

of a Banach algebra

The set of numbers for which is non-invertible (the algebra is assumed to be complex, is a given element of it and is the identity of the algebra). The spectrum is a non-empty compact set (the Gel'fand–Mazur theorem). In the case of a commutative algebra, the spectrum coincides with the set of values on this element of all the characters of the algebra (cf. Character of a -algebra).

This concept can be used as a basis for developing a functional calculus for the elements of a Banach algebra. The natural calculus of polynomials in an element of a Banach algebra is extended to a continuous homomorphism into from the ring of germs of functions holomorphic in a neighbourhood of the spectrum . The necessity of considering functions in several variables leads to the concept of the joint spectrum of a system of elements of a Banach algebra. 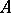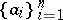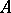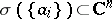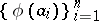If is commutative, then, by definition, the spectrum of a set of elements in is the collection of all -tuples of the form , where 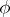is a character of 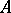. In general, one defines the left (right) spectrum of 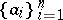to include those sets 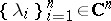for which the system is contained in a non-trivial left (respectively, right) ideal of the algebra. The spectrum is then defined as the union of the left and right spectra. For the basic results of multi-parametric spectral theory, and also for other approaches to the concept of the spectrum of a set of elements, see [1]–[4].

References

[1]	N. Bourbaki, "Theories spectrales" , Eléments de mathématiques , 32 , Hermann (1967)
[2]	R. Harte, "The spectral mapping theorem in several variables" Bull. Amer. Math. Soc. , 78 (1972) pp. 871–875
[3]	J. Taylor, "A joint spectrum for several commuting operators" J. Funct. Anal. , 6 (1970) pp. 172–191
[4]	W. Zhelazko, "An axiomatic approach to joint spectra I" Studia Math. , 64 (1979) pp. 249–261

References

[a1]	N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958)
[a2]	M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian)
[a3]	C.E. Rickart, "General theory of Banach algebras" , v. Nostrand (1960)