Spectrum of a ring
A topological space  whose points are the prime ideals
whose points are the prime ideals  of a ring
of a ring  with the Zariski topology (also called the spectral topology). It is assumed that
with the Zariski topology (also called the spectral topology). It is assumed that  is commutative and has an identity. The elements of
is commutative and has an identity. The elements of  can be regarded as functions on
can be regarded as functions on  by setting
by setting 
 .
.  supports a sheaf of local rings
supports a sheaf of local rings 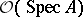 , called its structure sheaf. For a point
, called its structure sheaf. For a point 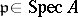 , the stalk of
, the stalk of 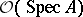 over
over 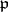 is the localization
is the localization 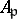 of
of 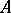 at
at 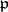 .
.
To any identity-preserving ring homomorphism 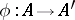 there corresponds a continuous mapping
there corresponds a continuous mapping 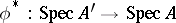 . If
. If 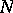 is the nil radical of
is the nil radical of 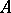 , then the natural mapping
, then the natural mapping 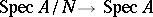 is a homeomorphism of topological spaces.
is a homeomorphism of topological spaces.
For a non-nilpotent element 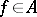 , let
, let 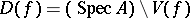 , where
, where 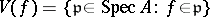 . Then the ringed spaces
. Then the ringed spaces 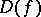 and
and 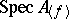 , where
, where  is the localization of
is the localization of 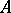 with respect to
with respect to 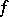 , are isomorphic. The sets
, are isomorphic. The sets 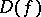 are called the principal open sets. They form a basis for the topology on
are called the principal open sets. They form a basis for the topology on 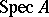 . A point
. A point 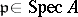 is closed if and only if
is closed if and only if 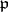 is a maximal ideal of
is a maximal ideal of 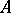 . By assigning to
. By assigning to 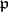 its closure
its closure 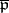 in
in  , one obtains a one-to-one correspondence between the points of
, one obtains a one-to-one correspondence between the points of 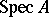 and the set of closed irreducible subsets of
and the set of closed irreducible subsets of 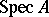 .
.  is quasi-compact, but usually not Hausdorff. The dimension of
is quasi-compact, but usually not Hausdorff. The dimension of 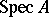 is defined as the largest
is defined as the largest  for which there is a sequence of distinct closed irreducible sets
for which there is a sequence of distinct closed irreducible sets 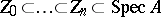 .
.
Many properties of 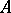 can be described in terms of
can be described in terms of 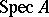 . For example,
. For example, 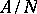 is Noetherian if and only if
is Noetherian if and only if 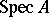 has the descending chain condition for closed sets;
has the descending chain condition for closed sets; 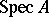 is an irreducible space if and only if
is an irreducible space if and only if 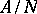 is an integral domain; the dimension of
is an integral domain; the dimension of 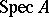 coincides with the Krull dimension of
coincides with the Krull dimension of 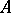 , etc.
, etc.
Sometimes one considers the maximal spectrum 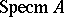 , which is the subspace of
, which is the subspace of 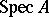 consisting of the closed points. For a graded ring
consisting of the closed points. For a graded ring 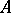 one also considers the projective spectrum
one also considers the projective spectrum 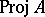 . If
. If 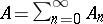 , then the points of
, then the points of 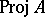 are the homogeneous prime ideals
are the homogeneous prime ideals 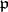 of
of 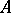 such that
such that 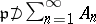 .
.
References
| [1] | N. Bourbaki, "Algèbre commutative" , Eléments de mathématiques , XXVIII , Hermann (1961) |
| [2] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
Comments
The continuous mapping 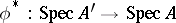 defined by a unitary ring homomorphism
defined by a unitary ring homomorphism 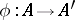 is given by
is given by 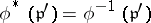 .
.
The pair  is an affine scheme.
is an affine scheme.
Similarly, 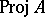 supports a sheaf of local rings
supports a sheaf of local rings 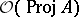 , the stalk of which at a point
, the stalk of which at a point 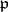 is the homogeneous localization
is the homogeneous localization 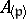 of
of 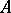 at
at 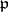 . (See also Localization in a commutative algebra.) The pair
. (See also Localization in a commutative algebra.) The pair 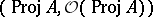 is a projective scheme.
is a projective scheme.
Spectra have also been studied for non-commutative rings, cf. [a1].
For Krull dimension see Dimension (of an associative ring).
References
| [a1] | F. van Oystaeyen, A. Verschoren, "Non-commutative algebraic geometry" , Lect. notes in math. , 887 , Springer (1981) |
Spectrum of a ring. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Spectrum_of_a_ring&oldid=15142